练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】等差数列{an}的前m项和为30，前2m项和为100，则它的前3m项和为（ ）
    A.130
    B.170
    C.210
    D.260

    【答案】C
    【解析】解：解法1：设等差数列{an}的首项为a1 ， 公差为d， 由题意得方程组 ，
    解得d= ，a1= ，
    ∴s3m=3ma1+ d=3m + =210．
    故选C．
    解法2：∵设{an}为等差数列，
    ∴sm ， s2m﹣sm ， s3m﹣s2m成等差数列，
    即30，70，s3m﹣100成等差数列，
    ∴30+s3m﹣100=70×2，
    解得s3m=210．
    故选C．
    【考点精析】掌握等差数列的前n项和公式和等差数列的性质是解答本题的根本，需要知道前n项和公式：；在等差数列{an}中，从第2项起，每一项是它相邻二项的等差中项；相隔等距离的项组成的数列是等差数列．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，DE∥BC，BC=2DE，CA⊥CB，CA⊥CD，CB⊥CD，F、G分别是AC、BC中点．
    （1）求证：平面DFG∥平面ABE；
    （2）若AC=2BC=2CD=4，求二面角E﹣AB﹣C的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一个单位有职工800人，期中具有高级职称的160人，具有中级职称的320人，具有初级职称的200人，其余人员120人．为了解职工收入情况，决定采用分层抽样的方法，从中抽取容量为40的样本．则从上述各层中依次抽取的人数分别是（ ）
    A.12，24，15，9
    B.9，12，12，7
    C.8，15，12，5
    D.8，16，10，6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，设向量 =（a， ）， =（cosC，c﹣2b），且 ⊥ ．
    （Ⅰ）求角A的大小；
    （Ⅱ）若a=1，求△ABC的周长l的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足：a1= ，a2= ，2an=an+1+an﹣1（n≥2，n∈N），数列{bn}满足：b1＜0，3bn﹣bn﹣1=n（n≥2，n∈R），数列{bn}的前n项和为Sn ．
    （1）求证：数列{bn﹣an}为等比数列；
    （2）求证：数列{bn}为递增数列；
    （3）若当且仅当n=3时，Sn取得最小值，求b1的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若把函数y=sin（ωx﹣ ）的图象向左平移 个单位，所得到的图象与函数y=cosωx的图象重合，则ω的一个可能取值是（ ）
    A.2
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}是等差数列，若 ＜﹣1，且它的前n项和Sn有最大值，那么当Sn取的最小正值时，n=（ ）
    A.11
    B.17
    C.19
    D.21

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，正三角形ABC的边长为2，D、E、F分别在三边AB，BC和CA上，且D为AB的中点，∠EDF=90°，∠BDE=θ（0°＜θ＜90°）．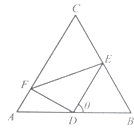
    （1）当tan∠DEF= 时，求θ的大小；
    （2）求△DEF的面积S的最小值及使得S取最小值时θ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂利用辐射对食品进行灭菌消毒，现准备在该厂附近建一职工宿舍，并对宿舍进行防辐射处理，建房防辐射材料的选用与宿舍到工厂距离有关．若建造宿舍的所有费用p（万元）和宿舍与工厂的距离x（km）的关系为：p= （0≤x≤8），若距离为1km时，宿舍建造费用为100万元．为了交通方便，工厂与宿舍之间还要修一条道路，已知购置修路设备需5万元，铺设路面每公里成本为6万元，设f（x）为建造宿舍与修路费用之和．
    （1）求f（x）的表达式，并写出其定义域；
    （2）宿舍应建在离工厂多远处，可使总费用f（x）最小，并求最小值．

    查看答案和解析>>

    同步练习册答案