
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,设向量 ![]() =(a,
=(a, ![]() ),
), ![]() =(cosC,c﹣2b),且
=(cosC,c﹣2b),且 ![]() ⊥
⊥ ![]() .
.
(Ⅰ)求角A的大小;
(Ⅱ)若a=1,求△ABC的周长l的取值范围.
【答案】解:(Ⅰ)由题意 ![]() ⊥
⊥ ![]() .可知:
.可知: ![]() , 即acosC+
, 即acosC+ ![]() =b,得sinAcosC+
=b,得sinAcosC+ ![]() sinC=sinB.
sinC=sinB.
又sinB=sin(A+C)=sinAcosB+cosAsinC.
∴ ![]() ,∵sinC≠0,∴cosA=
,∵sinC≠0,∴cosA= ![]() .
.
又0<A<π∴A= ![]() .
.
(Ⅱ)由正弦定理得:b= ![]() ,
, ![]() ,
,
l=a+b+c=1+ ![]() =1+
=1+ ![]()
=1+2( ![]() )
)
=1+2sin(B+ ![]() ).
).
∵A= ![]() .
.
∴B∈ ![]() ,∴B+
,∴B+ ![]() ,
,
∴sin(B+ ![]() )
) ![]() .
.
故△ABC的周长l的范围为(2,3]
【解析】(Ⅰ)利用向量的垂直,推出数量积为0,通过三角形内角和以及两角和的正弦函数,确定角A的大小;(Ⅱ)若a=1,利用正弦定理求出b、c的表达式,通过三角形的内角和以及两角和的正弦函数化简表达式,根据角的范围,确定三角函数的范围,然后求△ABC的周长l的取值范围.
【考点精析】本题主要考查了数量积判断两个平面向量的垂直关系的相关知识点,需要掌握若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直才能正确解答此题.
两平面的法向量垂直才能正确解答此题.


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD是平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EB= ![]() ,EF=1,BC=
,EF=1,BC= ![]() ,且M是BD的中点..
,且M是BD的中点.. 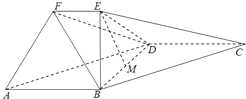
(1)求证:EM∥平面ADF;
(2)求直线DF和平面ABCD所成角的正切值;
(3)求二面角D﹣AF﹣B的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x,y满足不等式组  ,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
,若z=ax+y的最大值为2a+4,最小值为a+1,则实数a的取值范围为( )
A.[﹣1,2]
B.[﹣2,1]
C.[﹣3,﹣2]
D.[﹣3,1]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cos(ωx+ ![]() )(其中ω>0,x∈R)的最小正周期为10π.
)(其中ω>0,x∈R)的最小正周期为10π.
(1)求ω的值;
(2)设α,β∈[0, ![]() ],f(5α+
],f(5α+ ![]() )=﹣
)=﹣ ![]() ,f(5β﹣
,f(5β﹣ ![]() )=
)= ![]() ,求cos(α+β)的值.
,求cos(α+β)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:
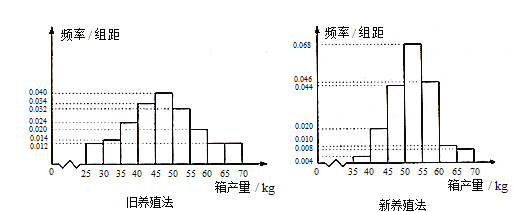
(1) 记A表示事件“旧养殖法的箱产量低于50kg”,估计A的概率;
(2) 填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50kg | 箱产量≥50kg | |
旧养殖法 | ||
新养殖法 |
(3) 根据箱产量的频率分布直方图,对两种养殖方法的优劣进行较。
附:
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,BC⊥平面APC,AB=2 ![]() ,AP=PC=CB=2.
,AP=PC=CB=2. 
(1)求证:AP⊥平面PBC;
(2)求二面角P﹣AB﹣C的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com