
���� ��I����x=��cos�ȣ�y=��sin�ȣ��������ߦ�2cos2��+3��2sin2��=3���ɻ�Ϊֱ�����귽�̣�����C2����������$\left\{\begin{array}{l}{x=-\sqrt{3}t}\\{y=1+t}\end{array}\right.$��tΪ������ ��ȥ������Ϊֱ�����귽�̣�
��II��ֱ�߷�������Բ���������ɵý������꣬�����е����깫ʽ��Բ�ı����̼��ɵó���
��� �⣺��I�����ߦ�2cos2��+3��2sin2��=3��Ϊֱ�����귽��Ϊ��x2+3y2=3����$\frac{{x}^{2}}{3}+{y}^{2}$=1��
����C2����������$\left\{\begin{array}{l}{x=-\sqrt{3}t}\\{y=1+t}\end{array}\right.$��tΪ������ ��Ϊֱ�����귽��Ϊ��x=-$\sqrt{3}$��y-1������x+$\sqrt{3}$y-$\sqrt{3}$=0��
��II��$\left\{\begin{array}{l}{{x}^{2}+3{y}^{2}=3}\\{x=-\sqrt{3}��y-1��}\end{array}\right.$�����$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$��$\left\{\begin{array}{l}{x=\sqrt{3}}\\{y=0}\end{array}\right.$
��A��0��1����B��$\sqrt{3}$��0�����߶�AB���е�ΪM$��\frac{\sqrt{3}}{2}��\frac{1}{2}��$����
���߶�ABΪֱ����Բ��ֱ�����귽��Ϊ $��x-\frac{\sqrt{3}}{2}��^{2}+��y-\frac{1}{2}��^{2}$=1��
���� ���⿼���˼����껯Ϊֱ�����ꡢ���Ǻ�����ֵ���е����깫ʽ��һԪ���η��̵ĸ���ϵ���Ĺ�ϵ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��${\sqrt{3}$��0�� | B�� | ��${\root{3}{4}$��2] | C�� | [${\root{3}{4}$��2�� | D�� | [${\root{3}{4}$��2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+b��0 | B�� | a-b��0 | C�� | $\frac{1}{a}$��$\frac{1}{b}$ | D�� | ab��b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
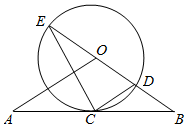 ��ͼ��ֱ��AB����ԲO�ϵĵ�C������OA=OB��CA=CB��ԲO��ֱ��OB�ڵ�E��D������EC��CD����tan��CED=$\frac{1}{2}$����O�İ뾶Ϊ3��
��ͼ��ֱ��AB����ԲO�ϵĵ�C������OA=OB��CA=CB��ԲO��ֱ��OB�ڵ�E��D������EC��CD����tan��CED=$\frac{1}{2}$����O�İ뾶Ϊ3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
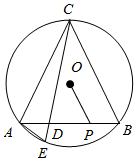 ��ͼ����֪AB�ǡ�O���ң�P��AB��һ�㣮
��ͼ����֪AB�ǡ�O���ң�P��AB��һ�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
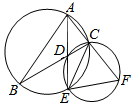 ��ͼ����BAC��ƽ������BC�͡�ABC�����Բ�ֱ��ཻ��D��E���ӳ�AC����D��E��C�����Բ�ڵ�F��
��ͼ����BAC��ƽ������BC�͡�ABC�����Բ�ֱ��ཻ��D��E���ӳ�AC����D��E��C�����Բ�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 45 | B�� | 48 | C�� | 25 | D�� | 28 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com