练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    下列说法：

      （1）命题“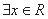，使得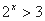”的否定是“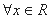，使得”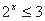

      （2）命题“函数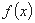在处有极值，则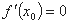”的否命题是真命题

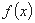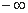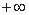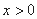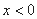      （3）是（，0）∪（0，）上的奇函数，时的解析式是，则 的解析式为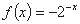

        其中正确的说法的个数是（    ）

    A．0个          B. 1个          C. 2个              D. 3个


    C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设为奇函数，为常数．

    （1）求的值；

    （2）判断函数在上的单调性，并说明理由；

    （3）若对于区间上的每一个值，不等式恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若，则f(－3)的值为(　　)

    A．2          B．8         C.          D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知定义在R上的奇函数f(x)有最小正周期2，且当x∈(0,1)时，f(x)＝.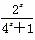

    (1)求f(1)和f(－1)的值；

    (2)求f(x)在[－1,1]上的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    条件，条件，则p是q的（     ）

    A．充分不必要条件B．必要不充分条件 充要条件  D．既不充分又不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知两曲线参数方程分别为 和，它们的交点坐标为________­­­­­­­­­­_________

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知定义在上的三个函数，，，且在处取得极值．

    （Ⅰ）求a的值及函数的单调区间.

    （Ⅱ）求证：当时，恒有成立.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某市2013年发放汽车牌照12万张，其中燃油型汽车牌照10万张，电动型汽车2万张．为了节能减排和控制总量，从2013年开始，每年电动型汽车牌照按50%增长，而燃油型汽车牌照每一年比上一年减少万张，同时规定一旦某年发放的牌照超过15万张，以后每一年发放的电动车的牌照的数量维持在这一年的水平不变．

    （1）记2013年为第一年，每年发放的燃油型汽车牌照数构成数列，每年发放的电动型汽车牌照数为构成数列，完成下列表格，并写出这两个数列的通项公式；

    （2）从2013年算起，求二十年发放的汽车牌照总量．

         

           

       

    3

         

            

       

    查看答案和解析>>

    科目：高中数学 来源： 题型：


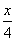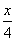     已知函数f(x)＝2sincos＋cos.

    (1)求函数f(x)的最小正周期及最值；

    (2)令g(x)＝f 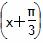，判断函数g(x)的奇偶性，并说明理由．

    查看答案和解析>>

    同步练习册答案