
如图,已知⊙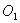 与⊙
与⊙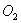 外切于点
外切于点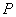 ,
, 是两圆的外公切线,
是两圆的外公切线,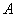 ,
,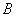 为切点,
为切点, 与
与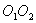 的延长线相交于点
的延长线相交于点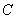 ,延长
,延长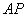 交⊙
交⊙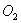 于 点
于 点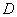 ,点
,点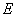 在
在 延长线上.
延长线上.
(1)求证: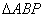 是直角三角形;
是直角三角形;
(2)若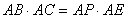 ,试判断
,试判断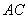 与
与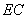 能否一定垂直?并说明理由.
能否一定垂直?并说明理由.
(3)在(2)的条件下,若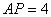 ,
,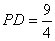 ,求
,求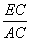 的值.
的值.


(1)证明略;(2)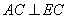 ;(3)
;(3)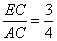
【解析】
试题分析:(1)从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线,平分两条切线的夹角;(2)判断三角形相似:一是平行于三角形一边的直线截其它两边所在的直线,截得的三角形与原三角形相似;二是如果一个三角形的两个角与另一个三角形的两个角对应相等, 那么这两个三角形相似;三是如果两个三角形的两组对应边的比相等,并且相应的夹角相等, 那么这两个三角形相似;四是如果两个三角形的三组对应边的比相等,那么这两个三角形相似;五是对应角相等,对应边成比例的两个三角形叫做相似三角;(3)切割线定理:切割线定理,是圆幂定理的一种,从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.
试题解析:解:(1)证明:过点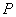 作两圆公切线
作两圆公切线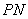 交
交 于
于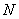 ,由切线长定理得
,由切线长定理得
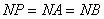 ,∴
,∴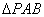 为直角三角形 3分
为直角三角形 3分
(2)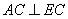
证明:∵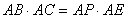 ,
,
∴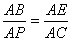 ,又
,又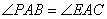 ,
,
∴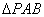 ∽
∽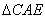
∴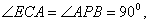 即
即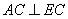 . 6分
. 6分
(3)由切割线定理,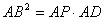 ,
,
∴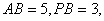
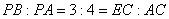
∴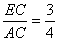 . 9分
. 9分
考点:(1)切线长定理;(2)相似三角形的应用;(3)切割线定理的应用.


科目:高中数学 来源: 题型:
有关部门从甲、乙两个城市所有的自动售货机中随机抽取了16台,记录了上午8∶00~11∶00之间各自的销售情况(单位:元)
甲:18,8,10,43,5,30,10,22,6,27,25,58,14,18,30,41;
乙:22,31,32,42,20,27,48,23,38,43,12,34,18,10,34,23.
试用两种不同的方式分别表示上面的数据,并简要说明各自的优点.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数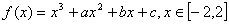 表示过原点的曲线,且在
表示过原点的曲线,且在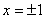 处的切线的倾斜角均为
处的切线的倾斜角均为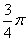 ,有以下命题:
,有以下命题:
①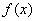 的解析式为
的解析式为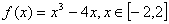 ;
;
②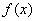 的极值点有且只有一个;
的极值点有且只有一个;
③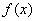 的最大值与最小值之和等于零;
的最大值与最小值之和等于零;
其中正确命题的序号为_ .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知100件产品中有5件次品,从这100件产品任意取出3件,设A表示事件“3件产品全不是次品”,B表示事件“3件产品全是次品”,C表示事件“3件产品中至少有1件次品”,则下列结论正确的是( )
A.B与C互斥
B.A与C互斥
C.A、B、C任意两个事件均互斥
D.A、B、C任意两个事件均不互斥
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com