
���� ���������ı���A1B1A2B2�����Ϊ$4\sqrt{3}$���Ƴ�$ab=2\sqrt{3}$�������ı���A1B1A2B2����Բ���̣�Բ�ģ�0��0����ֱ��A2B2�ľ���Ϊ$\frac{{2\sqrt{3}}}{{\sqrt{7}}}$�����a��b��Ȼ�������Բ���̣�
������M��x1��y1����N��x2��y2��������$\left\{{\begin{array}{l}{y=kx+m}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$�������б�ʽ�Լ�Τ�ﶨ����ͨ��$\overrightarrow{{A_2}M}•\overrightarrow{{A_2}N}=0$�����km��ϵʽ��Ȼ�����ֱ�߷���Ϊ$y=k��x-\frac{2}{7}��$���õ��������$��\frac{2}{7}��0��$��
��� ����С������13�֣�
�⣺�����ı���A1B1A2B2�����Ϊ$4\sqrt{3}$���ҿ�֪�ı���A1B1A2B2Ϊ���Σ�
��$\frac{1}{2}��2a•2b=4\sqrt{3}$����$ab=2\sqrt{3}$�١���2�֣�
������ɵ�ֱ��A2B2����Ϊ��$\frac{x}{a}+\frac{y}{b}=1$����bx+ay-ab=0��
���ı���A1B1A2B2����Բ����Ϊ${x^2}+{y^2}=\frac{12}{7}$��
��Բ�ģ�0��0����ֱ��A2B2�ľ���Ϊ$\frac{{2\sqrt{3}}}{{\sqrt{7}}}$����$\frac{|-ab|}{{\sqrt{{a^2}+{b^2}}}}=\frac{{2\sqrt{3}}}{{\sqrt{7}}}$�ڡ���4�֣�
�ɢ٢ڣ�a=2��$b=\sqrt{3}$��
����ԲC�ķ���Ϊ��$\frac{x^2}{4}+\frac{y^2}{3}=1$����6�֣�
������M��x1��y1����N��x2��y2����
��$\left\{{\begin{array}{l}{y=kx+m}\\{\frac{x^2}{4}+\frac{y^2}{3}=1}\end{array}}\right.$���3+4k2��x2+8mkx+4��m2-3��=0��
��ֱ��l����ԲC�ཻ��M��N������ͬ�ĵ㣬
���=64m2k2-16��3+4k2����m2-3����0�ã�3+4k2-m2��0��
��Τ�ﶨ����${x_1}+{x_2}=-\frac{8mk}{{3+4{k^2}}}��{x_1}{x_2}=\frac{{4��{m^2}-3��}}{{3+4{k^2}}}$����8�֣���
����MNΪֱ����Բ����ԲC���Ҷ���A2����A2M��A2N��$\overrightarrow{{A_2}M}•\overrightarrow{{A_2}N}=0$
����A2��2��0�������ԣ�x1-2��y1��•��x2-2��y2��=��x1-2����x2-2��+y1y2=0
⇒��x1-2����x2-2��+��kx1+m����kx2+m��=0
$⇒��{k^2}+1��{x_1}{x_2}+��mk-2����{x_1}+{x_2}��+{m^2}+4=0$
�Ӷ�$��{k^2}+1����\frac{{4��{m^2}-3��}}{{3+4{k^2}}}+��mk-2����-\frac{8mk}{{3+4{k^2}}}��+{m^2}+4=0$
��7m2+16mk+4k2=0��m=-2k����$m=-\frac{2}{7}k$�ʺϢۡ���11�֣�
��m=-2kʱ��ֱ��l��y=kx-2k����y=k��x-2����
���Ժ�����㣨2��0����
�ߣ�2��0��Ϊ��Բ���Ҷ��㣬�����ⲻ������ȥ��
��$m=-\frac{2}{7}k$ʱ��ֱ��l��$y=kx-\frac{2}{7}k$����$y=k��x-\frac{2}{7}��$��
���Ժ������$��\frac{2}{7}��0��$��
���Ͽ�֪��ֱ��l�����㣬�ö���Ϊ$��\frac{2}{7}��0��$������13�֣�
���� ���⿼��ֱ������Բ��λ�ù�ϵ��ֱ��ϵ���̵�Ӧ�ã�����ת��˼���Լ��������Ľ��ⷽ���������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
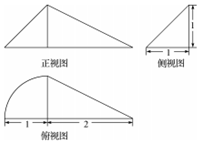
| A�� | $\frac{��}{6}+\frac{1}{3}$ | B�� | $\frac{��}{12}+1$ | C�� | $\frac{��}{12}+\frac{1}{3}$ | D�� | $\frac{��}{4}+\frac{1}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
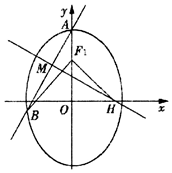 ��֪��ԲC��$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1��{a��b��0}��$���ϡ��½���ֱ�ΪF1��F2���Ͻ���F1��ֱ�� 4x+3y+12=0�ľ���Ϊ3����ԲC��������e=$\frac{1}{2}$��
��֪��ԲC��$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1��{a��b��0}��$���ϡ��½���ֱ�ΪF1��F2���Ͻ���F1��ֱ�� 4x+3y+12=0�ľ���Ϊ3����ԲC��������e=$\frac{1}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���⡰?x0��R��sinx0��1���ķ��ǡ�?x��R��sinx��1�� | |
| B�� | ����xy=0����x=0��y=0���������������x��0��y��0����xy��0�� | |
| C�� | �ڡ�ABC�У�A��B��sinA��sinB�ij�ֲ���Ҫ���� | |
| D�� | ��p�ģ��Vq��Ϊ�٣�p�ţ��Vq��Ϊ�棬��p��qͬ���ͬ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
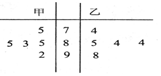 ��ͼ��ij��ס�����λͬѧ��5�ν��Լ���е���ѧ�ɼ����ٷ��ƣ��ľ�Ҷͼ���ס�����λͬѧ�÷ֵ���λ���ֱ�Ϊx1��x2���÷ֵķ���ֱ�Ϊy1��y2�������н�����ȷ���ǣ�������
��ͼ��ij��ס�����λͬѧ��5�ν��Լ���е���ѧ�ɼ����ٷ��ƣ��ľ�Ҷͼ���ס�����λͬѧ�÷ֵ���λ���ֱ�Ϊx1��x2���÷ֵķ���ֱ�Ϊy1��y2�������н�����ȷ���ǣ�������| A�� | x1��x2��y1��y2 | B�� | x1��x2��y1��y2 | C�� | x1��x2��y1��y2 | D�� | x1��x2��y1��y2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ������ | ����һ | ���ڶ� | ������ | ������ | ������ |
| ���г���β�� | 0��5 | 1��6 | 2��7 | 3��8 | 4��9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com