
已知函数 ,
, .
.
(1)求 在点
在点 处的切线方程;
处的切线方程;
(2)证明: 曲线 与曲线
与曲线 有唯一公共点;
有唯一公共点;
(3)设 ,比较
,比较 与
与 的大小, 并说明理由.
的大小, 并说明理由.
(1)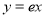 ;(2)祥见解析; (3)
;(2)祥见解析; (3)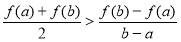 .
.
【解析】
试题分析:(1)由于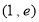 为切点,利用导数的几何意义求出x=1处的切线的斜率,利用点斜式求出切线方程,化成一般式即可;(2)要证两曲线有唯一公共点,只须证两个函数的差函数有唯一零点,注意到差函数在x=0处的函数值为零,所以只须用导数证明此函数在R上是一单调函数即可;(3)要比较两个式子的大小,一般用比差法:作差,然后对差式变形,最后确定差式的符号.此题作差后字母较多,注意观察,可构造函数,用导数对函数的单调性进行研究,从而达到确定符号的目的.
为切点,利用导数的几何意义求出x=1处的切线的斜率,利用点斜式求出切线方程,化成一般式即可;(2)要证两曲线有唯一公共点,只须证两个函数的差函数有唯一零点,注意到差函数在x=0处的函数值为零,所以只须用导数证明此函数在R上是一单调函数即可;(3)要比较两个式子的大小,一般用比差法:作差,然后对差式变形,最后确定差式的符号.此题作差后字母较多,注意观察,可构造函数,用导数对函数的单调性进行研究,从而达到确定符号的目的.
试题解析:(1)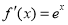 ,则
,则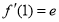 ,
,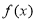 点
点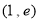 处的切线方程为:
处的切线方程为: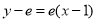 ,即
,即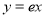
(2)令 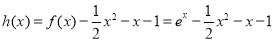 ,
,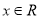 ,则
,则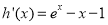 ,
,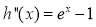 ,且
,且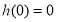 ,
, ,
,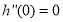 因此,
因此,
当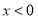 时,
时,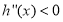 ,
,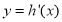 单调递减;
单调递减;
当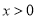 时,
时,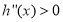 ,
,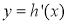 单调递增.
单调递增.
所以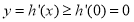 ,所以
,所以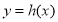 在
在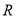 上单调递增,又
上单调递增,又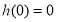 ,即函数
,即函数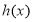 有唯一零点
有唯一零点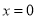 ,
,
所以曲线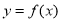 与曲线
与曲线 有唯一公共点
有唯一公共点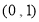 .
.
(3)设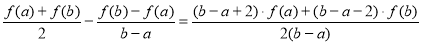
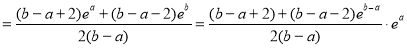
令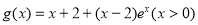 ,则
,则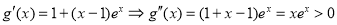 ,
,
所以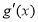 在
在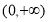 上单调递增,且
上单调递增,且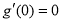 ,因此
,因此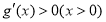 ,从而
,从而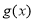 在
在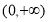 上单调递增,而
上单调递增,而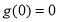 ,所以在
,所以在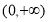 上
上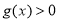 ;即当
;即当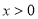 时,
时, 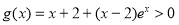 ,又因为
,又因为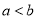 ,所以有
,所以有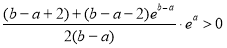 ;所以当
;所以当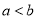 时,
时, 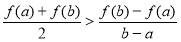 .
.
考点:1.导数的几何意义;2.导数研究函数的单调性.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届山东省济宁市高二5月质量检测文科数学试卷(解析版) 题型:选择题
函数f(x)= +
+ 的定义域为( )
的定义域为( )
A.[-2,0)∪(0,2] B.(-1,0)∪(0,2] C.[-2,2] D.(-1,2]
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:选择题
已知椭圆C: 的离心率为
的离心率为 .双曲线
.双曲线 的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
的渐近线与椭圆C有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆C的方程为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:选择题
已知盒中装有3个红球、2个白球、5个黑球,它们大小形状完全相同,现需一个红球,甲每次从中任取一个不放回,在他第一次拿到白球的条件下,第二次拿到红球的概率( )
A.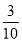 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测文科数学试卷(解析版) 题型:填空题
关于函数 ,有下列命题
,有下列命题
①由 ,可得
,可得 必是
必是 的整数倍;
的整数倍;
② 的表达式可改写成
的表达式可改写成 ;
;
③ 的图象关于点
的图象关于点 对称;
对称;
④ 的图象关于直线
的图象关于直线 对称.其中正确命题的序号为 .
对称.其中正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源:2015届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:填空题
椭圆 的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若
的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若 成等比数列,则此椭圆的离心率为________.(离心率
成等比数列,则此椭圆的离心率为________.(离心率 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com