
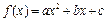 ,其中
,其中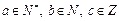 .
.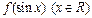 的最大值为2,最小值为-4,试求函数f(x)的最小值;
的最大值为2,最小值为-4,试求函数f(x)的最小值;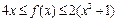 恒成立,且存在
恒成立,且存在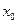 使得
使得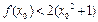 成立,求c的值.
成立,求c的值. 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
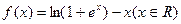 有下列性质:“若
有下列性质:“若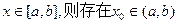 ,使得
,使得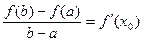 ”成立。
”成立。 唯一;
唯一; 图象上三个不同的点,试判断△ABC的形状,并说明理由。
图象上三个不同的点,试判断△ABC的形状,并说明理由。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

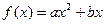 对任意
对任意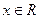 均有
均有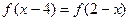 成立,且函数的图像过点
成立,且函数的图像过点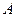
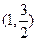 .
.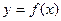 的解析式;
的解析式;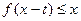 的解集为
的解集为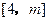 ,求实数
,求实数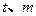 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
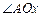 的内部,
的内部,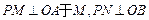 于N,四边形ONPM的面积为2..
于N,四边形ONPM的面积为2..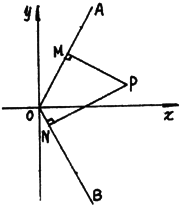 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
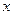 与人均消费
与人均消费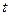 (元)的关系如下:
(元)的关系如下: 
 万元(不含工作人员的工资),还要上缴占旅游收入20%的税收,其余自负盈亏.目前公园的工作人员维持在40人.要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?
万元(不含工作人员的工资),还要上缴占旅游收入20%的税收,其余自负盈亏.目前公园的工作人员维持在40人.要使工作人员平均每人每天的工资不低于100元,并维持每天正常运营(不负债),每天的游客人数应控制在怎样的合理范围内?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com