
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
科目:高中数学 来源: 题型:解答题
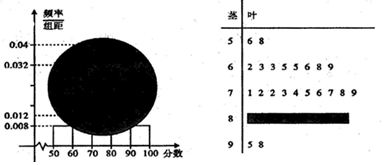
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 平均每天足球运动的时间 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,2.5) | [2.5,3] |
| 人数 | 2 | 3 | 28 | 22 | 10 | x |
| 平均每天足球运动的时间 | [0,0.5) | [0.5,1) | [1,1.5) | [1.5,2) | [2,2.5) | [2.5,3] |
| 人数 | 5 | 12 | 18 | 10 | 3 | y |
| 足球健将 | 非足球健将 | 总 计 | |
| 男 生 | |||
| 女 生 | |||
| 总 计 |
| P(K2>k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,圆锥的高$PO=\sqrt{2}$,底面⊙O的直径AB=2,C是圆上一点,且∠CAB=30°,D为AC的中点,则直线OC和平面PAC所成角的正弦值为( )
如图,圆锥的高$PO=\sqrt{2}$,底面⊙O的直径AB=2,C是圆上一点,且∠CAB=30°,D为AC的中点,则直线OC和平面PAC所成角的正弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{21}{2}$ | B. | -$\frac{63}{8}$ | C. | $\frac{63}{8}$ | D. | $\frac{63}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com