
分析 (I)运用数列递推式:当n=1时,a1=S1;n≥2时,an=Sn-Sn-1.化简整理即可得到所求通项公式;
(II)求得bn=log2an=log22×4n-1=2n-1,$\frac{1}{{b}_{k}{b}_{k+1}}$=$\frac{1}{(2k-1)(2k+1)}$=$\frac{1}{2}$($\frac{1}{2k-1}$-$\frac{1}{2k+1}$),运用数列的求和方法:裂项相消求和,即可得到所求和.
解答 解:(I)当n=1时,3a1=3S1=2×4-2=6,解得a1=2;
n≥2时,an=Sn-Sn-1=$\frac{1}{3}$(2×4n-2-2×4n-1+2)=2×4n-1.
当n=1时也成立.
则数列{an}的通项公式an=2×4n-1.
(II)bn=log2an=log22×4n-1=2n-1,
$\frac{1}{{b}_{k}{b}_{k+1}}$=$\frac{1}{(2k-1)(2k+1)}$=$\frac{1}{2}$($\frac{1}{2k-1}$-$\frac{1}{2k+1}$),
则Tn=$\frac{1}{{b}_{1}{b}_{2}}$+$\frac{1}{{b}_{2}{b}_{3}}$+…+$\frac{1}{{b}_{n}{b}_{n+1}}$=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$.
点评 本题考查数列的通项公式的求法,注意运用数列递推式:当n=1时,a1=S1;n≥2时,an=Sn-Sn-1.考查数列的求和方法:裂项相消求和,化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{3\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
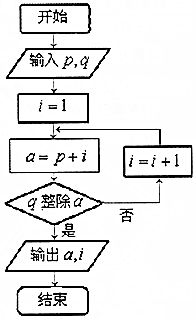 阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )
阅读如图所示的程序框图,若输入p=2,q=9,则输出的a、i的值分别为( )| A. | a=3,i=1 | B. | a=18,i=16 | C. | a=18,i=15 | D. | a=9,i=7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com