
���� ��1���Լ���ѡ����Ŀ�������ۣ�����������¼��ĸ��ʼ��㹫ʽ���ɵó��״��سɹ��ĸ��ʣ�
��2����ס��Ҵ��سɹ��ֱ�Ϊ�¼�A��B����P��$\overline{A}$��=$\frac{{∁}_{4}^{1}{∁}_{2}^{2}}{{∁}_{6}^{3}}$��P��$\overline{B}$��=$��1-\frac{2}{3}��^{3}+{∁}_{3}^{2}��\frac{2}{3}����1-\frac{2}{3}��^{2}$���ɵüס���������һ�˴��سɹ��ĸ�����1-P��$\overline{A}\overline{B}$��=1-$P��\overline{A}��P��\overline{B}��$��
��3��������ɵã��Ρ�B$��3��\frac{2}{3}��$��P����=k��=${∁}_{3}^{k}��\frac{2}{3}��^{k}��\frac{1}{3}��^{3-k}$�����ɵó���
��� �⣺��1���״��سɹ��ĸ���P=$\frac{{∁}_{4}^{1}}{{∁}_{6}^{1}}��\frac{{∁}_{3}^{1}}{{∁}_{5}^{1}}$+$\frac{{∁}_{4}^{1}}{{∁}_{6}^{1}}��\frac{{∁}_{2}^{1}}{{∁}_{5}^{1}}��\frac{{∁}_{3}^{1}}{{∁}_{4}^{1}}$+$\frac{{∁}_{2}^{1}}{{∁}_{6}^{1}}��\frac{{∁}_{4}^{2}}{{∁}_{5}^{2}}$=$\frac{4}{5}$��
��2����ס��Ҵ��سɹ��ֱ�Ϊ�¼�A��B��
��P��$\overline{A}$��=$\frac{{∁}_{4}^{1}{∁}_{2}^{2}}{{∁}_{6}^{3}}$=$\frac{1}{5}$��P��$\overline{B}$��=$��1-\frac{2}{3}��^{3}+{∁}_{3}^{2}��\frac{2}{3}����1-\frac{2}{3}��^{2}$=$\frac{7}{27}$��
��ס���������һ�˴��سɹ��ĸ�����1-P��$\overline{A}\overline{B}$��=1-$P��\overline{A}��P��\overline{B}��$=1-$\frac{1}{5}��\frac{7}{27}$=$\frac{128}{135}$��
��3��������ɵã��Ρ�B$��3��\frac{2}{3}��$��P����=k��=${∁}_{3}^{k}��\frac{2}{3}��^{k}��\frac{1}{3}��^{3-k}$��
| �� | 0 | 1 | 2 | 3 |
| P | $\frac{1}{27}$ | $\frac{6}{27}$ | $\frac{12}{27}$ | $\frac{8}{27}$ |
���� ���⿼���������������¼��ĸ��ʼ��㹫ʽ������ֲ��е����ʼ�����ѧ������������������������������������е��⣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
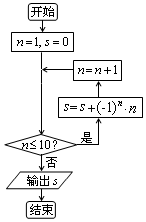
| A�� | -6 | B�� | 6 | C�� | -5 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
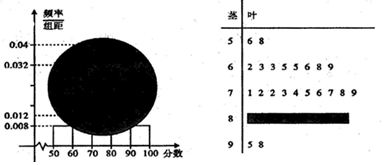
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ۢ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com