
分析 (1)当a=b=4时,方程x3+4x2+4x+c=0有三个不同实根,等价于函数f(x)=x3+4x2+4x+c=0有三个不同零点,由f(x)的单调性知,当且仅当$c∈(0,\frac{32}{27})$时,函数f(x)=x3+4x2+4x+c有三个不同零点,可得结论;
(2)若函数f(x)有三个不同零点,则必有△=4a2-12b>0,故a2-3b>0是f(x)有三个不同零点的必要条件,再证明充分性即可.
解答 解:设f(x)=x3+ax2+bx+c.
(1)当a=b=4时,方程x3+4x2+4x+c=0有三个不同实根,等价于函数f(x)=x3+4x2+4x+c=0有三个不同零点,f'(x)=3x3+8x+4,令f'(x)=0得x1=-2或${x_2}=-\frac{2}{3}$,f(x)与f'(x)的区间(-∞,+∞)上情况如下:
| x | (-∞,-2) | -2 | (-2,-$\frac{2}{3}$) | -$\frac{2}{3}$ | (-$\frac{2}{3}$,+∞) |
| f(x) | + | 0 | - | 0 | + |
| f'(x) | c | c-$\frac{32}{27}$ |
点评 本题考查导数知识的综合运用,考查函数的单调性,考查函数的零点,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
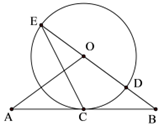 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (f(1)+1)•e>f(2)+1 | B. | 3e<f(2)+1 | ||
| C. | 3•e≥f(1)+1 | D. | 3e2与f(2)+1大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若p∨q为真命题,则p∧q为真命题 | |
| B. | “x=5”是“x2-4x-5=0”的充分不必要条件 | |
| C. | 命题“若x<-1,则x2-2x-3>0”的否命题为:“若x<-1,则x2-2x-3≤0” | |
| D. | 已知命题p:?x∈R,x2+x-1<0,则¬p:?x∈R,x2+x-1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{3\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com