
���� ��1��������C1�ķ��̻�Ϊ��ͨ���̣�Ȼ��ת�����C1�ļ����귽�̣�
��2������l�IJ�������Ϊ$\left\{\begin{array}{l}x=tcos��\\ y=tsin��\end{array}$��$\frac{��}{2}$�������У�tΪ������t��0������Ϊy=xtan����������ɵã�|OA|=��1=2cos����|OB|=��2=4cos��������|AB|=$\sqrt{3}$�����ɵó���
��� �⣺��1������C1�IJ�������Ϊ$\left\{\begin{array}{l}x=1+cos��\\ y=sin��\end{array}$����Ϊ��������
�ɵã�x-1��2+y2=1��x=��cos�ȣ�y=��sin�ȣ�
��C1�ļ����귽��Ϊ��2-2��cos��=0��
����=2cos�ȣ�
��2������l�IJ�������Ϊ$\left\{\begin{array}{l}x=tcos��\\ y=tsin��\end{array}$��$\frac{��}{2}$�������У�tΪ������t��0������Ϊy=xtan����
������ɵã�|OA|=��1=2cos����|OB|=��2=4cos����
��|AB|=$\sqrt{3}$��
��|OA|-|OB|=-2cos��=$\sqrt{3}$����cos��=-$\frac{\sqrt{3}}{2}$��
��$\frac{��}{2}$��������
���=$\frac{5��}{6}$��
���� ���⿼����ֱ�������뼫����Ļ������������̻�Ϊ��ͨ���̡�����֮��ľ��롢Բ�����ʣ�������������������������������е��⣮


 ���100��1�ž�ϵ�д�
���100��1�ž�ϵ�д� ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | 6 | C�� | 9 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ?x��R��x2��0 | B�� | $?{x_0}��R��{x_0}^2��0$ | C�� | $?{x_0}��R��{x_0}^2��0$ | D�� | $?{x_0}��R��{x_0}^2��0$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
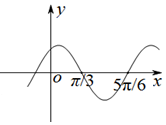 ��֪����f��x��=sin����x+�գ����أ�0��0���գ��У���ͼ����ͼ��ʾ����f��x����ͼ������ƽ��$\frac{��}{6}$����λ���õ�g��x����ͼ������g��x���Ľ���ʽΪ��������
��֪����f��x��=sin����x+�գ����أ�0��0���գ��У���ͼ����ͼ��ʾ����f��x����ͼ������ƽ��$\frac{��}{6}$����λ���õ�g��x����ͼ������g��x���Ľ���ʽΪ��������| A�� | g��x��=sin2x | B�� | g��x��=cos2x | C�� | $g��x��=sin��2x+\frac{��}{6}��$ | D�� | $g��x��=sin��2x+\frac{2��}{3}��$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com