
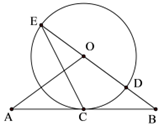
 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.分析 (1)利用等腰三角形的性质和切线的定义即可证明;
(2)利用直径所对的圆周角为直角及正切函数的定义可得$\frac{CD}{EC}$=$\frac{1}{2}$.再利用切线的性质可得△CBD∽△EBC,于是$\frac{BD}{BC}$=$\frac{CD}{EC}$=$\frac{1}{2}$.设BD=x,BC=2x,利用切割线定理可得BC2=BD•BE,代入解出即可.
解答 解: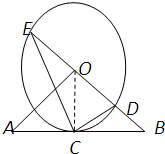 (1)证明:如图,连接OC,
(1)证明:如图,连接OC,
∵OA=OB,CA=CB,
∴OC⊥AB,
∴AB是⊙O的切线;
(2)∵ED是直径,∴∠ECD=90°,
在Rt△ECD中,∵tan∠CED=$\frac{1}{2}$,
∴$\frac{CD}{EC}$=$\frac{1}{2}$.
∵AB是⊙O的切线,
∴∠BCD=∠E.
又∵∠CBD=∠EBC,
∴△CBD∽△EBC,
∴$\frac{BD}{BC}$=$\frac{CD}{EC}$=$\frac{1}{2}$.
设BD=x,BC=2x,
又BC2=BD•BE,∴(2x)2=x•(x+4).
解得:x1=0,x2=$\frac{4}{3}$,
∵BD=x>0,∴BD=$\frac{4}{3}$.
∴OA=OB=BD+OD=$\frac{4}{3}$+2=$\frac{10}{3}$.
点评 本题考查了等腰三角形的性质、切线的定义、圆的性质、相似三角形的性质、切割线定理等基础知识与基本技能方法,考查了推理能力和计算能力,属于中档题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
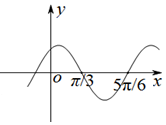 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )| A. | g(x)=sin2x | B. | g(x)=cos2x | C. | $g(x)=sin(2x+\frac{π}{6})$ | D. | $g(x)=sin(2x+\frac{2π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com