
分析 (1)直线l无斜率时,直线l的方程为x=1,成立;直线l有斜率时,设方程为kx-y-k=0,由圆心到直线的距离等于半径,能求出直线l的方程.
(2)△CPQ面积最大时,△CPQ是等腰直角三角形,此时圆心到直线的距离为$\sqrt{2}$,设直线l的方程为kx-y-k=0,由此能求出直线l的方程.
解答 解:(1)直线l无斜率时,直线l的方程为x=1,
此时直线l和圆C相切.
直线l有斜率时,设方程为y=k(x-1),即kx-y-k=0,
∵l与圆C相切,∴圆心到直线的距离等于半径,
即$d=\frac{{|{3k-4-k}|}}{{\sqrt{{k^2}+1}}}=2$,
解得k=$\frac{3}{4}$,∴直线l的方程为$y=\frac{3}{4}x-\frac{3}{4}$
(2)△CPQ面积最大时,∠PCQ=90°,$S=\frac{1}{2}×2×2=2$,
即△CPQ是等腰直角三角形,
由半径r=2得:圆心到直线的距离为$\sqrt{2}$
设直线l的方程为:y=k(x-1),即kx-y-k=0,
则$d=\frac{{|{2k-4}|}}{{\sqrt{{k^2}+1}}}=\sqrt{2}$,∴k=7或k=1,
∴直线l的方程为:y=7x-7,y=x-1.
点评 本题考查直线方程的求法、直线与椭圆位置关系,本题突出对运算能力、化归转化能力的考查,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{27}$ | B. | $\frac{8π}{27}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
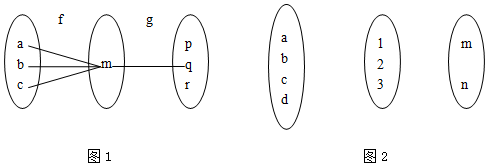
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
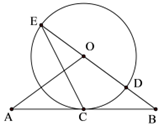 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若p∨q为真命题,则p∧q为真命题 | |
| B. | “x=5”是“x2-4x-5=0”的充分不必要条件 | |
| C. | 命题“若x<-1,则x2-2x-3>0”的否命题为:“若x<-1,则x2-2x-3≤0” | |
| D. | 已知命题p:?x∈R,x2+x-1<0,则¬p:?x∈R,x2+x-1≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com