
分析 (1)由已知得到等差数列{bn}的公差的方程解之;结合an2-2anan+1+an-2an+1=0,得到(an+1)an=2an+1(an+1),数列{an}是以1为首项$\frac{1}{2}$为公比的等比数列,得到通项公式.
(2)首项得到数列{cn}的通项公式,利用错位相减法求和.
解答 解:(1)因为等差数列{bn}a1=b1=1,b2+b4=10,满足an2-2anan+1+an-2an+1=0,
所以2b1+4d=10,解得d=2,所以bn=2n-1;
由an2-2anan+1+an-2an+1=0,得到(an+1)an=2an+1(an+1),
数列{an}各项都是正数,所以$\frac{{a}_{n+1}}{{a}_{n}}=\frac{1}{2}$,
所以数列{an}是以1为首项$\frac{1}{2}$为公比的等比数列,所以an=$\frac{1}{{2}^{n-1}}$.
(2)设cn=$\frac{1}{a_n}+{b_n}$=2n-1+2n-1,
所以数列{cn}的前n项和${S}_{n}=({2}^{0}+{2}^{1}+{2}^{2}+…+{2}^{n-1})$+2(1+2+3+…+n)-n
=$\frac{1-{2}^{n}}{1-2}+2×\frac{n(n+1)}{2}-n$=2n+n2-1.
点评 本题考查了等差数列和等比数列通项公式的求法以及利用错位相减法对数列求和;属于经常考查题型.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:选择题
| x | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| y1 | 5 | 130 | 505 | 1130 | 2005 | 3130 | 4505 |
| y2 | 5 | 94.478 | 1785.2 | 33733 | 6.37×105 | 1.2×107 | 2.28×108 |
| y3 | 5 | 30 | 55 | 80 | 105 | 130 | 155 |
| y4 | 5 | 2.3107 | 1.4295 | 1.1407 | 1.0461 | 1.0151 | 1.005 |
| A. | y2、y1 | B. | y2、y3 | C. | y4、y3 | D. | y1、y3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
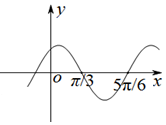 已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的图象如图所示,将f(x)的图象向左平移$\frac{π}{6}$个单位,得到g(x)的图象,则函数g(x)的解析式为( )| A. | g(x)=sin2x | B. | g(x)=cos2x | C. | $g(x)=sin(2x+\frac{π}{6})$ | D. | $g(x)=sin(2x+\frac{2π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com