
���� ��1�������⣬$\frac{1}{2}��\frac{x}{\frac{3}{2}}��2$��$\frac{1}{2}��\frac{4}{x}��2$���������x��ȡֵ��Χ��
��2�������⣬an=a1+��n-1��d��$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{a}_{1}+nd}{{a}_{1}+��n-1��d}$=1+$\frac{1}{\frac{{a}_{1}}{d}+n-1}$$��1��\frac{1}{2}$�����ݡ��������С��Ķ��弴��֤�����ۣ�
��3�����蹫����q���жϳ�q��1���ɵȱ����е�ͨ�ʽ��ǰn���ʽ����$\frac{{a}_{n+1}}{{a}_{n}}$��$\frac{{S}_{n+1}}{{S}_{n}}$�����ݡ��������С��Ķ����г�����ʽ�飬���������q��ȡֵ��Χ��
��� �⣺��1�������⣬$\frac{1}{2}��\frac{x}{\frac{3}{2}}��2$��$\frac{1}{2}��\frac{4}{x}��2$����2��x��3��
��x��ȡֵ��Χ��[2��3]��
��2�������⣬an=a1+��n-1��d����$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{{a}_{1}+nd}{{a}_{1}+��n-1��d}$=1+$\frac{1}{\frac{{a}_{1}}{d}+n-1}$$��1��\frac{1}{2}$��
$\frac{{a}_{n+1}}{{a}_{n}}$����n���������С�����Ե�n=1ʱ��$\frac{{a}_{n+1}}{{a}_{n}}$ȡ�����ֵ����$\frac{{a}_{n+1}}{{a}_{n}}$��2��
��{an}�ǡ��������С���
��3��������ã��ȱ�����{an}�Ĺ���q
��q��1ʱ������an=a1qn-1��Sn=$\frac{{a}_{1}��1-{q}^{n}��}{1-q}$��$\frac{{S}_{n+1}}{{S}_{n}}$=$\frac{1-{q}^{n+1}}{1-{q}^{n}}$��
��Ϊ����{an}��{Sn}���ǡ��������С�������$\frac{1}{2}��q��2$��$\frac{1}{2}��$$\frac{1-{q}^{n+1}}{1-{q}^{n}}$��2�����$\frac{1}{2}��q��1$��
��q=1ʱ��an=a1��Sn=na1���� $\frac{{a}_{n+1}}{{a}_{n}}$=1��$\frac{{S}_{n+1}}{{S}_{n}}$=1+$\frac{1}{n}$�ʣ�1��$\frac{3}{2}$]���������⣬
��q��ȡֵ��Χ��$[\frac{1}{2}��1]$��
���� �������¶����⣬�������е�an��Sn�Ĺ�ϵʽ���ȱ����е�ͨ�ʽ��ǰn���ʽ������Ĺؼ�����ȷ�����¶��岢��Ӧ�ã�


 �ƸԾ���Ȥζ����ϵ�д�
�ƸԾ���Ȥζ����ϵ�д� ����С����ҵ��ϵ�д�
����С����ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}+\frac{1}{2}i$ | B�� | $\frac{1}{4}+\frac{1}{2}i$ | C�� | $\frac{2}{5}+\frac{2}{5}i$ | D�� | $\frac{1}{5}+\frac{2}{5}i$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 25 | B�� | 5 | C�� | -15 | D�� | -20 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
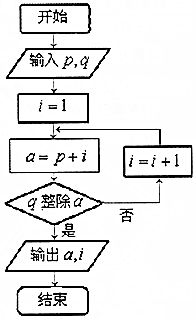 �Ķ���ͼ��ʾ�ij����ͼ��������p=2��q=9���������a��i��ֵ�ֱ�Ϊ��������
�Ķ���ͼ��ʾ�ij����ͼ��������p=2��q=9���������a��i��ֵ�ֱ�Ϊ��������| A�� | a=3��i=1 | B�� | a=18��i=16 | C�� | a=18��i=15 | D�� | a=9��i=7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com