
分析 点A(a,b)和点B(0,3)在直线1:3x-4y+5=0的同侧,则(3a-4b+5)×(3×0-4×3+5)>0,即3a-4b+5<0,作出点A(a,b) 对应的平面区域,利用目标函数的几何意义结合数形结合进行判断即可
解答 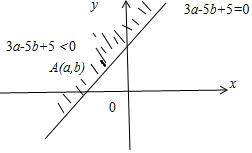 解:点A(a,b)和点B(0,3)在直线1:3x-4y+5=0的同侧,
解:点A(a,b)和点B(0,3)在直线1:3x-4y+5=0的同侧,
则(3a-4b+5)×(3×0-4×3+5)>0,即3a-4b+5<0,点A(a,b)的区域如图所示.
对于①,若a>1,由3a-4b+5<0;可得b>2,故正确;
对于②,∵原点到直线3a-4b+5=0的距离等于1,∴$\sqrt{{a}^{2}+{b}^{2}}$>1,故正确;
对于③,函数f(x)=sinx-3a+4b-4零点,就是y=sinx与y=3a-4b+4的交点,∵y=3a-4b+4>-1,故错;
对于④,当b<0时,$\frac{b-1}{a}$表示过点A(a,b)与点(0,1)的斜率,根据图象可得其取值范围是(0,$\frac{3}{4}$),故正确.
故答案为:①②④.
点评 本题考查的知识点是二元一次不等式与平面区域,考查转化思想与运算能力,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
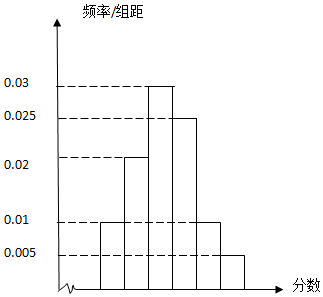 某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示
某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示| P(K2≥k0) | 0.01 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧q | B. | p∧(¬q) | C. | (¬p)∨q | D. | ¬(p∨q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $0<a<\frac{1}{2}$ | B. | $\frac{1}{3}<a<\frac{1}{2}$ | C. | $0<a<\frac{1}{3}$ | D. | a>1或$0<a<\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
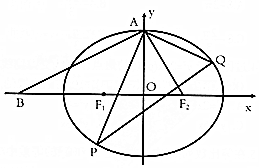 设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,上顶点为A,在x轴负半轴上有一点B,满足$\overrightarrow{B{F}_{1}}$=$\overrightarrow{{F}_{1}{F}_{2}}$,且$\overrightarrow{AB}$•$\overrightarrow{A{F}_{2}}$=0.
设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,上顶点为A,在x轴负半轴上有一点B,满足$\overrightarrow{B{F}_{1}}$=$\overrightarrow{{F}_{1}{F}_{2}}$,且$\overrightarrow{AB}$•$\overrightarrow{A{F}_{2}}$=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 若正整数n除以正整数m后的余数为N,则记为n≡N(bmodm),例如10≡4(bmod6),下面程序框图的算法源于我国古代闻名中外的“中国剩余定理”,执行该程序框图,则输出的n等于( )
若正整数n除以正整数m后的余数为N,则记为n≡N(bmodm),例如10≡4(bmod6),下面程序框图的算法源于我国古代闻名中外的“中国剩余定理”,执行该程序框图,则输出的n等于( )| A. | 11 | B. | 13 | C. | 14 | D. | 17 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com