
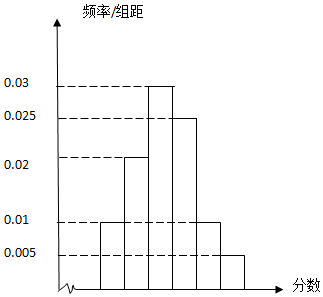
 某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示
某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示| P(K2≥k0) | 0.01 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
分析 (Ⅰ)根据题意,计算平均数即可;
(Ⅱ)根据分层抽样原理计算从这四组中分别抽取的人数,
填写列联表,计算观测值,对照临界值表得出结论.
解答 解:(Ⅰ)根据题意,计算平均数为
$\overline{x}$=(45×0.01+55×0.02+65×0.03+75×0.025+85×0.01+95×0.005)×10=67;…(5分)
(Ⅱ)[60,70),[70,80),[80,90),[90,100]四组学生的频率之比为
0.3:0.25:0.1:0.05=6:5:2:1,
按分层抽样应该从这四组中分别抽取30,25,10,5人,
依题意,可得到以下列联表:
| 男生 | 女生 | 合计 | |
| 优异 | 4 | 1 | 5 |
| 一般(及格) | 32 | 33 | 65 |
| 合计 | 36 | 34 | 70 |
点评 本题考查了平均数与分层抽样原理的应用问题,也考查了独立性检验的应用问题,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3:4 | B. | 3:2 | C. | 1:1 | D. | 1:3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,若M为线段A1C的中点,则在△ADE翻转过程中,对于下列说法:
如图,矩形ABCD中,AB=2AD=2,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE,若M为线段A1C的中点,则在△ADE翻转过程中,对于下列说法:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com