练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．如图所示，在△ABC中，D为BC的中点，BP丄DA，垂足为P，且BP=2，则$\overrightarrow{BC}$•$\overrightarrow{BP}$=（　　）
    A．2B．4C．8D．16

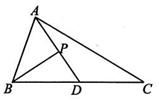
    分析 由D为中点，可得$\overrightarrow{BC}$=2$\overrightarrow{BD}$，再由向量的数量积的定义和解直角三角形的知识，即可得到所求值．

    解答 解：在△ABC中，D为BC的中点，BP丄DA，垂足为P，且BP=2，
    则$\overrightarrow{BC}$•$\overrightarrow{BP}$=2$\overrightarrow{BD}$•$\overrightarrow{BP}$=2|$\overrightarrow{BP}$|•|$\overrightarrow{BD}$|•cos∠DBP=2|$\overrightarrow{BP}$|2=2×4=8．
    故选：C．

    点评 本题考查向量在三角形的运用，考查数量积的定义的运用，以及运算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．已知实数x，y满足不等式组$\left\{\begin{array}{l}{x≥0}\\{x+y≤2}\\{y≥x}\end{array}\right.$，若目标函数z=kx+y仅在点（1，1）处取得最小值，则实数k的取值范围是  （　　）
    A．（-1，+∞）B．（-∞，-1）C．（1，+∞）D．（-∞，1）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

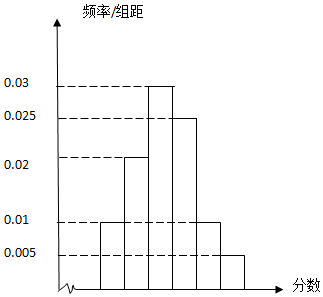    15．某地十余万考生的成绩中，随机地抽取了一批考生的成绩，将其分为6组：第一组[40，50），第二组[50，60），…，第六组[90，100]，作出频率分布直方图，如图所示
    （I）用每组区间的中点值代表该组的数据，估算这批考生的平均成绩；
    （II）现从及格的学生中，用分层抽样的方法抽取了70名学生（其中女生有34名），已知成绩“优异”（超过90分）的女生有1名，能否有95%的把握认为数学成绩优异与性别有关？
    附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
    P（K2≥k0）0.010.050.0250.010
    k02.7063.8415.0246.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在区间[-1，m]上随机选取一个数x，若x≤1的概率为$\frac{2}{5}$，则实数m的值为（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知函数f（x）=alnx+x2-x，其中a∈R．
    （Ⅰ）若a＜0，讨论f（x）的单调性；
    （Ⅱ）当x≥1时，f（x）≥0恒成立，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．下面命题判断正确的是（　　）
    A．若p∨q是真命题，则p，q都是真命题
    B．命题“?x0∈R，x02-1＞0的否定是“?x∈R，x2-1＜0”
    C．过平面α外的一点P的直线与平面α所成的角为θ，则这样的直线有无数条
    D．△ABC中，“A＞B”是“sinA＞sinB”的充要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知命题p：?x∈R，x2-2xsinθ+1≥0；命题q：?α，β∈R，sin（α+β）≤sinα+sinβ，则下列命题中的真命题为（　　）
    A．（￢p）∧qB．p∧（￢q）C．（￢p）∨qD．￢（p∨q）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知函数$f（x）=\left\{\begin{array}{l}{a^x}，\;0＜x≤1\;\\{log_a}x\;，x＞1\end{array}\right.$（a＞0且a≠1），若f（3a2）＞f（1-2a），则a的取值范围是（　　）
    A．$0＜a＜\frac{1}{2}$B．$\frac{1}{3}＜a＜\frac{1}{2}$C．$0＜a＜\frac{1}{3}$D．a＞1或$0＜a＜\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

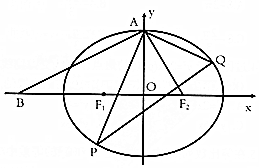    14．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1、F2，上顶点为A，在x轴负半轴上有一点B，满足$\overrightarrow{B{F}_{1}}$=$\overrightarrow{{F}_{1}{F}_{2}}$，且$\overrightarrow{AB}$•$\overrightarrow{A{F}_{2}}$=0．
    （Ⅰ）求椭圆C的离心率；
    （Ⅱ）若D是经过A、B、F2三点的圆上的点，且D到直线l：x-$\sqrt{3}$y-3=0的最大距离等于椭圆长轴的长，求椭圆C的方程；
    （Ⅲ）在（Ⅱ）的条件下，设P、Q是椭圆C上异于A的两点，且以PQ为直径的圆过点A，问直线PQ是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由．

    查看答案和解析>>

    同步练习册答案