
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
分析 设M(x,y),由$\overrightarrow{OM}•\overrightarrow{OA}=\overrightarrow{OF}•\overrightarrow{OA}$⇒cx+by=c2,…①,由$\overrightarrow{OM}+\overrightarrow{OF}=t\overrightarrow{OA}({t∈R})$,cy-bx=bc…②
由①②得x=$\frac{{a}^{2}c-2{b}^{2}c}{{a}^{2}}$,y=$\frac{2b{c}^{2}}{{a}^{2}}$,…③
把③代入椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$得a4c2+4c6=a6⇒2c3=b3+bc2,c3-b3=bc2-c3,
⇒(c-b)(b2+bc+2c2)=0⇒b=c.
解答 解:设M(x,y),∵$\overrightarrow{OM}•\overrightarrow{OA}=\overrightarrow{OF}•\overrightarrow{OA}$∴$\overrightarrow{OA}•(\overrightarrow{OM}-\overrightarrow{OF)}=0$,⇒$\overrightarrow{OA}•\overrightarrow{FM}=0$
⇒即OA⊥MF⇒cx+by=c2,…①
.$\overrightarrow{OM}+\overrightarrow{OF}=(x+c,y)$,因为$\overrightarrow{OM}+\overrightarrow{OF}=t\overrightarrow{OA}({t∈R})$,$\overrightarrow{OM}+\overrightarrow{OF}与\overrightarrow{OA}$共线,cy-bx=bc…②
由①②得x=$\frac{{a}^{2}c-2{b}^{2}c}{{a}^{2}}$,y=$\frac{2b{c}^{2}}{{a}^{2}}$,…③
把③代入椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$得a4c2+4c6=a6⇒2c3=b3+bc2,c3-b3=bc2-c3,
⇒(c-b)(b2+bc+2c2)=0⇒b=c
⇒a=$\sqrt{2}c$,椭圆的离心率e=$\frac{c}{a}=\frac{\sqrt{2}}{2}$.
故选:A
点评 本题考查了向量与圆锥曲线的综合应用,及向量的线性运算、转化思想,属于难题.


科目:高中数学 来源: 题型:解答题
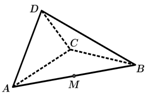 如图,在三棱锥A-BCD中,AD=DC=2,AD⊥DC,AC=CB,AB=4,平面ADC⊥平面ABC,M为AB的中点.
如图,在三棱锥A-BCD中,AD=DC=2,AD⊥DC,AC=CB,AB=4,平面ADC⊥平面ABC,M为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,+∞) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.48 | B. | 0.6 | C. | 0.75 | D. | 0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
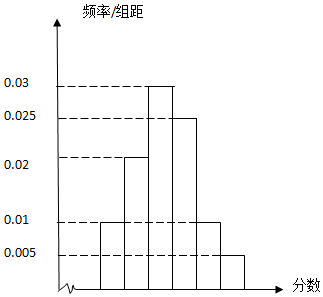 某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示
某地十余万考生的成绩中,随机地抽取了一批考生的成绩,将其分为6组:第一组[40,50),第二组[50,60),…,第六组[90,100],作出频率分布直方图,如图所示| P(K2≥k0) | 0.01 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∧q | B. | p∧(¬q) | C. | (¬p)∨q | D. | ¬(p∨q) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com