Question

10．已知半径为1的球O内切于正四面体A-BCD，线段MN是球O的一条动直径（M，N是直径的两端点），点P是正四面体A-BCD的表面上的一个动点，则$\overrightarrow{PM}•\overrightarrow{PN}$的取值范围是[0，8]．

Answer 1

分析 运用向量的加减运算和数量积的性质：向量的平方即为模的平方，讨论P位于切点E和顶点时分别取得最值，即可得到所求取值范围．

解答 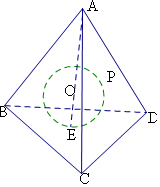解：由题意M，N是直径的两端点，可得$\overrightarrow{OM}$+$\overrightarrow{ON}$=$\overrightarrow{0}$，$\overrightarrow{OM}$•$\overrightarrow{ON}$=-1，
则$\overrightarrow{PM}•\overrightarrow{PN}$=（$\overrightarrow{PO}$+$\overrightarrow{OM}$）•（$\overrightarrow{PO}$+$\overrightarrow{ON}$）=$\overrightarrow{PO}$²+$\overrightarrow{PO}$•（$\overrightarrow{OM}$+$\overrightarrow{ON}$）+$\overrightarrow{OM}$•$\overrightarrow{ON}$
=$\overrightarrow{PO}$²+0-1=$\overrightarrow{PO}$²-1，
即求正四面体表面上的动点P到O的距离的范围．
当P位于E（切点）时，OP取得最小值1；
当P位于A处时，OP即为正四面体外接球半径最大即为3．
设正四面体的边长为a，由O为正四面体的中心，
可得直角三角形ABE中，AE=$\frac{\sqrt{6}}{3}$a，BE=$\frac{\sqrt{3}}{3}$a，OE=$\frac{\sqrt{6}}{12}$a，AO=$\frac{\sqrt{6}}{4}$a，
综上可得$\overrightarrow{PO}$²-1的最小值为1-1=0，最大值为9-1=8．
则$\overrightarrow{PM}•\overrightarrow{PN}$的取值范围是[0，8]．
故答案为：[0，8]．

点评 本题考查向量在几何中的运用，考查向量的加减运算和数量积的性质，考查运算能力，属于中档题．