
【题目】如图,在平面直角坐标系xOy中,已知椭圆![]() (a>b>0)的左、右焦点分别为F1,F2,过点F2的直线交椭圆于M,N两点.已知椭圆的短轴长为
(a>b>0)的左、右焦点分别为F1,F2,过点F2的直线交椭圆于M,N两点.已知椭圆的短轴长为![]() ,离心率为
,离心率为![]() .
.

(1)求椭圆的标准方程;
(2)当直线MN的斜率为![]() 时,求
时,求![]() 的值;
的值;
(3)若以MN为直径的圆与x轴相交的右交点为P(t,0),求实数t的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() .
.
【解析】
(1)设焦距2c,由题得到关于![]() 的方程组,解方程组即得解;
的方程组,解方程组即得解;
(2)先求出点![]() 的坐标,再利用两点间的距离公式得解;
的坐标,再利用两点间的距离公式得解;
(3)先讨论当直线MN斜率不存在时,![]() ;再讨论直线
;再讨论直线![]() 斜率存在的情况,联立直线和椭圆方程得到韦达定理,再根据
斜率存在的情况,联立直线和椭圆方程得到韦达定理,再根据![]() 得到
得到![]() ,解不等式组综合即得解.
,解不等式组综合即得解.
解:(1)设焦距2c,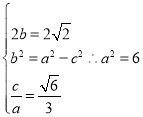 ,
,![]() ,
,
故椭圆的标准方程为:![]() ;
;
(2)由(1)知,c=2,则F2(2,0)
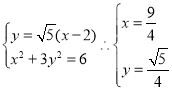 或
或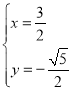
即![]() ,或
,或![]() ,
,
因此,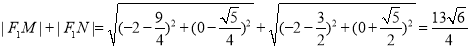 ;
;
(3)当直线MN斜率不存在时,MN:x=2,![]() =
=![]() ,
,
以MN为直径的圆方程为:![]() ,
,
其与x轴相交的右交点为(![]() ,0),即
,0),即![]() ;
;
当MN的斜率存在时,设MN:![]() ,M(
,M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() )
)
![]()
所以![]() ,
,
![]() ,
,![]() ,
,
则![]() ,
,
因为P在以MN为直径的圆上,则![]() ,
,
所以![]()
所以![]()
所以![]()
所以![]() ,
,
因为![]() ,
,
所以![]() .
.
∵P是右交点,故t>2,
因此![]() ,
,
解得![]() .
.
综合得![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱![]() (侧棱垂直于底面,且底面三角形
(侧棱垂直于底面,且底面三角形![]() 是等边三角形)中,
是等边三角形)中,![]() ,
,![]() 分别是
分别是![]() 的中点.
的中点.
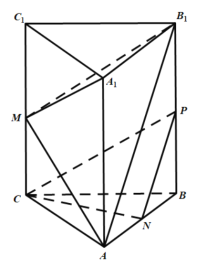
(1)求证:平面![]() ∥平面
∥平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() 使
使![]() 平面
平面![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,也请说明理由.
的位置;若不存在,也请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 存在极值,求实数a的取值范围;
存在极值,求实数a的取值范围;
(2)设![]() ,设
,设![]() 是定义在
是定义在![]() 上的函数.
上的函数.
(ⅰ)证明:![]() 在
在![]() 上为单调递增函数(
上为单调递增函数(![]() 是
是![]() 的导函数);
的导函数);
(ⅱ)讨论![]() 的零点个数.
的零点个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为某街区道路示意图,图中的实线为道路,每段道路旁的数字表示单向通过此段道路时会遇见的行人人数,在防控新冠肺炎疫情期间,某人需要从A点由图中的道路到B点,为避免人员聚集,此人选择了一条遇见的行人总人数最小的从A到B的行走线路,则此人从A到B遇见的行人总人数最小值是_________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点到直线
的焦点到直线![]() 的距离为
的距离为![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() 、
、![]() 两点.
两点.
(1)求抛物线![]() 的准线方程;
的准线方程;
(2)设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,若
,若![]() ,且
,且![]() 与
与![]() 的交点在抛物线
的交点在抛物线![]() 上,求直线
上,求直线![]() 的斜率和点
的斜率和点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】明代商人程大位在公元1592年编撰完成《算法统宗》一书.书中有如下问题:“今有女子善织,初日迟,次日加倍,第三日转速倍增,第四日又倍增,织成绢六丈七尺五寸.问各日织若干?”意思是:“有一位女子善于织布,第一天由于不熟悉有点慢,第二天起每天织的布都是前一天的2倍,已知她前四天共织布6丈7尺5寸,问这位女子每天织布多少?”根据文中的已知条件,可求得该女了第一天织布________尺,若织布一周(7天),共织________尺.(其中1丈为10尺,1尺为10寸)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过正四面体ABCD的顶点A作一个形状为等腰三角形的截面,且使截面与底面BCD所成的角为![]() ,这样的截面有( )
,这样的截面有( )
A.6个B.12个C.16个D.18个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | |||
女生 | |||
合计 | 120 |
(2)从被调查中对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
参考公式:附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com