【题目】已知抛物线
的焦点到直线
的距离为
，过点
的直线
与
交于
、
两点.
（1）求抛物线的准线方程；
（2）设直线
的斜率为
，直线
的斜率为
，若
，且
与的交点在抛物线上，求直线的斜率和点
的坐标.
科目：高中数学 来源： 题型：
【题目】东京夏季奥运会推迟至2021年7月23日至8月8日举行，此次奥运会将设置4
100米男女混泳接力赛这一新的比赛项目，比赛的规则是：每个参赛国家派出2男2女共计4名运动员参加比赛，按照仰泳
蛙泳蝶泳自由泳的接力顺序，每种泳姿100米且由1名运动员完成，且每名运动员都要出场.若中国队确定了备战该项目的4名运动员名单，其中女运动员甲只能承担仰泳或者自由泳，男运动员乙只能承担蝶泳或者蛙泳，剩下2名运动员四种泳姿都可以承担，则中国队参赛的安排共有（ ）
A.144种B.8种C.24种D.12种
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝axlnx﹣x2﹣ax+1（a∈R）在定义域内有两个不同的极值点.
（1）求实数a的取值范围；
（2）设两个极值点分别为x1，x2，x1＜x2，证明：f（x1）+f（x2）＜2﹣x12+x22.
查看答案和解析>>
科目：高中数学 来源： 题型：
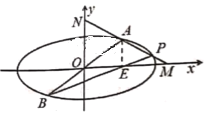
【题目】如图，已知椭圆C:
过原点的直线与椭圆交于A，B两点(点A在第一象限)，过点A作x轴的垂线，垂足为点
，设直线BE与椭圆的另一交点为P，连接AP得到直线l，交x轴于点M，交y轴于点N.
（1）若
，求直线AP的斜率；
（2）记
的面积分别为S1，S2，S3，求
的的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设数列
中前两项
给定，若对于每个正整数
，均存在正整数
（
）使得
，则称数列
为“
数列”.
（1）若数列为
的等比数列，当时，试问：
与
是否相等，并说明数列是否为“数列”；
（2）讨论首项为
、公差为
的等差数列是否为“数列”，并说明理由；
（3）已知数列为“数列”，且
，记
，
，其中正整数
， 对于每个正整数，当正整数分别取1、2、
、
时
的最大值记为
、最小值记为
. 设
，当正整数
满足
时，比较
与
的大小，并求出的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在平面直角坐标系xOy中，已知椭圆
(a＞b＞0)的左、右焦点分别为F1，F2，过点F2的直线交椭圆于M，N两点．已知椭圆的短轴长为
，离心率为
．
（1）求椭圆的标准方程；
（2）当直线MN的斜率为
时，求
的值；
（3）若以MN为直径的圆与x轴相交的右交点为P(t，0)，求实数t的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】高二某班共有45人，学号依次为1、2、3、…、45，现按学号用系统抽样的办法抽取一个容量为5的样本，已知学号为6、24、33的同学在样本中，那么样本中还有两个同学的学号应为（ ）
A.
B.
C.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
