
 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨)的几组对应数据:
(吨)的几组对应数据: | 3 | 4 | 5 | 6 |
 | 2.5 | 3 |  | 4.5 |
 对
对 的回归直线方程是
的回归直线方程是 0.7
0.7 +0.35,则表中
+0.35,则表中 的值为( )
的值为( ) 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源:不详 题型:解答题
 与销售额
与销售额 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据: | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.95% | B.99% | C.99.5% | D.99.9% |
| | 患心脏病 | 不患心脏病 | 合计 |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 其中n =" a" + b + c + d).
其中n =" a" + b + c + d).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示转速(单位转/秒),用
表示转速(单位转/秒),用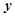 表示每小时生产的有缺点物件个数,现观测得到
表示每小时生产的有缺点物件个数,现观测得到 的4组观测值为(8,5),(12,8),(14,9),(16,11).
的4组观测值为(8,5),(12,8),(14,9),(16,11).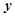 与
与 之间有线性相关关系,求
之间有线性相关关系,求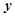 对
对 的回归直线方程.
的回归直线方程. )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x | 0 | 1 | 4 | 5 | 6 | 8 |
| y | 1.3 | 1.8 | 5.6 | 6.1 | 7.4 | 9.3 |
 =0.95x+a,则a=________.
=0.95x+a,则a=________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| x | 10 | 20 | 30 | 40 | 50 |
| y | 62 | ■ | 75 | 81 | 89 |
 =0.67x+54.9,现发现表中有一个数据模糊不清,请推断该点数据的值为( )
=0.67x+54.9,现发现表中有一个数据模糊不清,请推断该点数据的值为( )查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 =
= x+
x+ ,使代数式[y1-(
,使代数式[y1-( x1+
x1+ )]2+[y2-(
)]2+[y2-( x2+
x2+ )]2+[y3-(
)]2+[y3-( x3+
x3+ )]2的值最小时,
)]2的值最小时, =
= -
-
 ,
, =
= (
( ,
, 分别是这三组数据的横、纵坐标的平均数),
分别是这三组数据的横、纵坐标的平均数),| x | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| y | 4 | 6 | 5 | 6.2 | 8 | 7.1 | 8.6 |
 xi+
xi+ )|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.
)|≤0.2,即称(xi,yi)为(1)中回归直线的拟合“好点”,求后4组数据中拟合“好点”的概率.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com