
 表示转速(单位转/秒),用
表示转速(单位转/秒),用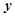 表示每小时生产的有缺点物件个数,现观测得到
表示每小时生产的有缺点物件个数,现观测得到 的4组观测值为(8,5),(12,8),(14,9),(16,11).
的4组观测值为(8,5),(12,8),(14,9),(16,11).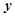 与
与 之间有线性相关关系,求
之间有线性相关关系,求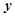 对
对 的回归直线方程.
的回归直线方程. )
) 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源:不详 题型:填空题
| 1 |
| n |
| n |
 |
| i=1 |
| . |
| x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | 10 | 8 | 6 | 5 |
 =-3.2x+
=-3.2x+ ,则
,则 =( )
=( )查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 和判断力
和判断力 进行统计分析,得下表数据:
进行统计分析,得下表数据: |  |  |  |  |
 |  |  |  |  |
 关于
关于 的线性回归方程
的线性回归方程 中的
中的 的值为
的值为 ,则记忆力为
,则记忆力为 的同学的判断力约为(附:线性回归方程
的同学的判断力约为(附:线性回归方程 中,
中, ,其中
,其中 、
、 为样本平均值)( )
为样本平均值)( ) B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨)的几组对应数据:
(吨)的几组对应数据: | 3 | 4 | 5 | 6 |
 | 2.5 | 3 |  | 4.5 |
 对
对 的回归直线方程是
的回归直线方程是 0.7
0.7 +0.35,则表中
+0.35,则表中 的值为( )
的值为( )查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A. =x+1 =x+1 | B. =x+2 =x+2 |
C. =2x+1 =2x+1 | D. =2x+2 =2x+2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 64 | 69 | 75 | 82 | 90 |
 ,根据回归方程,预测加工70个零件所花费的时间为________分钟.
,根据回归方程,预测加工70个零件所花费的时间为________分钟.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 物理 成绩好 | 物理 成绩不好 | 合计 |
| 数学成绩好 | 62 | 23 | 85 |
| 数学成绩不好 | 28 | 22 | 50 |
| 合计 | 90 | 45 | 135 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com