
 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:
已知二次函数f(x)=ax2-(a+2)x+1(a∈Z),且函数f(x)在(-2,-1)上恰有一个零点,则不等式f(x)>1的解集为( )
A.(-∞,-1)∪(0,+∞) B.(-∞,0)∪(1,+∞)
C.(-1,0) D.(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
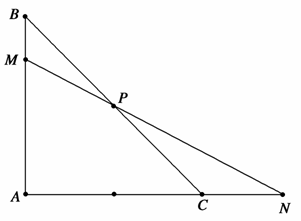
如图,在等腰直角△ABC中,点P是斜边BC的中点,过点P的直线分别交直线AB、AC于不同的两点M、N,若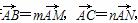 则mn的最大值为( )
则mn的最大值为( )
A.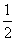 B.1 C.2 D.3
B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
为保增长、促发展,某地计划投资甲、乙两个项目,根据市场调研,知甲项目每投资100万元需要配套电能2万千瓦时,可提供就业岗位24个,GDP增长260万元;乙项目每投资100万元需要配套电能4万千瓦时,可提供就业岗位36个,GDP增长200万元.已知该地为甲、乙两个项目最多可投资3000万元,配套电能100万千瓦时,若要求两个项目能提供的就业岗位不少于840个,问如何安排甲、乙两个项目的投资额,才能使GDP增长的最多.
查看答案和解析>>
科目:高中数学 来源: 题型:
某工厂生产甲、乙两种产品,每种产品都有一部分是一等品,其余是二等品,已知甲产品为一等品的概率比乙产品为一等品的概率多0.25,甲产品为二等品的概率比乙产品为一等品的概率少0.05.
(1)分别求甲、乙产品为一等品的概率P甲,P乙;
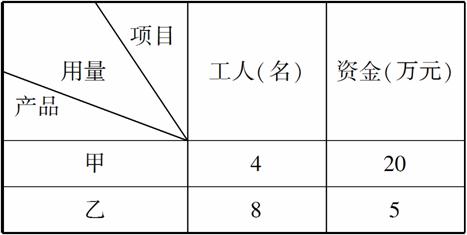
(2)已知生产一件产品需要用的工人数和资金数如表所示,且该厂有工人32名,可用资金55万元.设x,y分别表示生产甲、乙产品的数量,在(1)的条件下,求x,y为何值时,z=xP甲+yP乙最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
平行四边形ABCD的一条对角线固定在A(3,-1),C(2,-3)两点,D点在直线3x-y+1=0上移动,则B点的轨迹方程为( )
A.3x-y-20=0 B.3x-y-10=0
C.3x-y-9=0 D.3x-y-12=0
查看答案和解析>>
科目:高中数学 来源: 题型:
已知指数函数y=2x的图象与y轴交于点A,对数函数y=lgx的图象与x轴交于点B,点P在直线AB上移动,点M(0,-2),则|MP|的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如下图,定圆半径为a,圆心为C(b,c),则直线ax+by+c=0与直线x-y+1=0的交点在( )
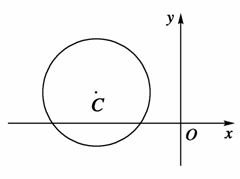
A.第一象限 B.第二象限
C.第三象限 D.第四象限
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com