
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)当a=1时,求函数![]() 的单调区间:
的单调区间:
(Ⅱ)求函数![]() 的极值;
的极值;
(Ⅲ)若函数![]() 有两个不同的零点,求a的取值范围。
有两个不同的零点,求a的取值范围。
【答案】(Ⅰ)单调减区间为(1,+![]() ) ,增区间为(0,1); (Ⅱ)见解析(Ⅲ)a>1
) ,增区间为(0,1); (Ⅱ)见解析(Ⅲ)a>1
【解析】
(Ⅰ)当a=1, f′(x)=![]() ,解f′(x)<0和f′(x)>0确定单调区间;(Ⅱ)f′(x)
,解f′(x)<0和f′(x)>0确定单调区间;(Ⅱ)f′(x)![]() ,讨论a≤0和a>0时f′(x)的符号,确定单调性和极值;(Ⅲ)由(Ⅱ)知当 a≤0时,f(x)至多有一个零点,舍去;当a>0时,函数的极小值为f(a)=
,讨论a≤0和a>0时f′(x)的符号,确定单调性和极值;(Ⅲ)由(Ⅱ)知当 a≤0时,f(x)至多有一个零点,舍去;当a>0时,函数的极小值为f(a)=![]() 设函数g(x)=lnx+x-1,求导确定g(x):当0<x<1时,g(x)<0;x>1时,g(x)>0,分情况讨论:当0<a≤1,f(a)=ag(a) ≤0,f(x)至多有一个零点,不符合题意;当a>1时,由零点存在定理确定(
设函数g(x)=lnx+x-1,求导确定g(x):当0<x<1时,g(x)<0;x>1时,g(x)>0,分情况讨论:当0<a≤1,f(a)=ag(a) ≤0,f(x)至多有一个零点,不符合题意;当a>1时,由零点存在定理确定(![]() )和(a,3a-1)各有一个零点,则a可求
)和(a,3a-1)各有一个零点,则a可求
(Ⅰ)当a=1时,![]() , f′(x)=
, f′(x)=![]()
当f′(x)<0时,x>1; f′(x)>0时,0<x<1
∴函数![]() 的单调减区间为(1,+
的单调减区间为(1,+![]() ) ,增区间为(0,1)
) ,增区间为(0,1)
(Ⅱ)f(x)的定义域是(0,+∞),
f′(x)![]() ,
,
若a≤0,则f′(x)<0,此时f(x)在(0,+∞)递减,无极值
若a>0,则由f′(x)=0,解得:x=a,
当0<x<a时,f′(x)>0,当x>a时,f′(x)<0,
此时f(x)在(0,a)递增,在(a,+∞)递减;
∴当x=a时,函数的极大值为f(a)=![]() ,无极小值
,无极小值
(Ⅲ)由(Ⅱ)可知
当 a≤0时,f(x)在(0,+∞)递减,则f(x)至多有一个零点,不符合题意,舍去;
当a>0时,函数的极小值为f(a)=![]() ,
,
令g(x)=lnx+x-1(x>0)
∵![]() ∴g(x)在(0,+∞)单调递增,又g(1)=0, ∴0<x<1时,g(x)<0;x>1时,g(x)>0
∴g(x)在(0,+∞)单调递增,又g(1)=0, ∴0<x<1时,g(x)<0;x>1时,g(x)>0
(i) 当0<a≤1,f(a)=ag(a) ≤0,则函数f(x)至多有一个零点,不符合题意,舍去;
(ii) 当a>1时,f(a)=ag(a)>0
∵![]() ∴函数f(x)在(
∴函数f(x)在(![]() )内有一个零点,
)内有一个零点,
∵f(3a-1)=aln(3a-1)-![]()
设h(x)=lnx-x(x>2)
∵![]() ∴h(x)在(2,+∞)内单调递减,则h(3a-1)<h(2)=ln2-2<0
∴h(x)在(2,+∞)内单调递减,则h(3a-1)<h(2)=ln2-2<0
∴函数f(x)在(a,3a-1)内有一个零点.则当a>1时,函数f(x)恰有两个零点
综上,函数![]() 有两个不同的零点时,a>1
有两个不同的零点时,a>1


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别是椭圆C:
分别是椭圆C:![]() 的左、右焦点,
的左、右焦点,![]() ,直线1过
,直线1过![]() 且垂直于x轴,交椭圆C于A、B两点,连接A、B、
且垂直于x轴,交椭圆C于A、B两点,连接A、B、![]() ,所组成的三角形为等边三角形。
,所组成的三角形为等边三角形。
(1)求椭圆C的方程;
(2)过右焦点![]() 的直线m与椭圆C相交于M、N两点,试问:椭圆C上是否存在点P,使
的直线m与椭圆C相交于M、N两点,试问:椭圆C上是否存在点P,使![]() 成立?若存在,求出点P的坐标;若不存在,说明理由.
成立?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的三棱锥称之为鳖臑。若三棱锥P-ABC为鳖臑,PA⊥面ABC,PA=AB=2,AC=4,三棱锥P-ABC的四个顶点都在球的球面上,则球0的表面积为( )
A. 8πB. 12πC. 20πD. 24π
查看答案和解析>>
科目:高中数学 来源: 题型:
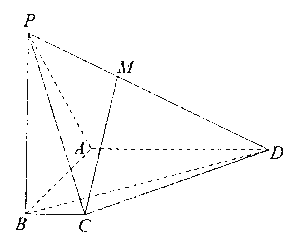
【题目】如图,在四棱锥![]() 中:
中:![]() 底面ABCD,底面ABCD为梯形,
底面ABCD,底面ABCD为梯形,![]() ,
,![]() ,且
,且![]() ,BC=1,M为棱PD上的点。
,BC=1,M为棱PD上的点。
(Ⅰ)若![]() ,求证:CM∥平面PAB;
,求证:CM∥平面PAB;
(Ⅱ)求证:平面![]() 平面PAB;
平面PAB;
(Ⅲ)求直线BD与平面PAD所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某度假酒店为了解会员对酒店的满意度,从中抽取50名会员进行调查,把会员对酒店的“住宿满意度”与“餐饮满意度”都分为五个评分标准:1分(很不满意);2分(不满意);3分(一般);4分(满意);5分(很满意).其统计结果如下表(住宿满意度为![]() ,餐饮满意度为
,餐饮满意度为![]() )
)

(1)求“住宿满意度”分数的平均数;
(2)求“住宿满意度”为3分时的5个“餐饮满意度”人数的方差;
(3)为提高对酒店的满意度,现从![]() 且
且![]() 的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
的会员中随机抽取2人征求意见,求至少有1人的“住宿满意度”为2的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图为我国数学家赵爽(约3世纪初)在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不相同,则不同的涂色方案共有( )
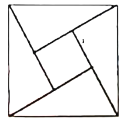
A.360种B.720种C.480种D.420种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,![]() E是PD的中点.
E是PD的中点.
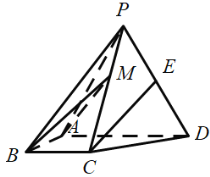
(1)证明:直线![]() 平面PAB;
平面PAB;
(2)点M在棱PC 上,且直线BM与底面ABCD所成角为![]() ,求二面角M-AB-D的余弦值.
,求二面角M-AB-D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com