
分析 当0<x<1时,f(x)=-lnx,f′(x)=-$\frac{1}{x}$∈(-∞,-1),当x>1时,f(x)=lnx,f′(x)=$\frac{1}{x}$∈(0,1),进而将x0=1和${x_0}=\frac{1}{2}$代入,结果斜率公式分类讨论可得答案.
解答 解:∵函数f(x)=|lnx|,
当0<x<1时,f(x)=-lnx,f′(x)=-$\frac{1}{x}$∈(-∞,-1),
当x>1时,f(x)=lnx,f′(x)=$\frac{1}{x}$∈(0,1),
①当x0=1时,f(x)-f(x0)≥c(x-x0)可化为:f(x)-f(1)≥c(x-1)
当0<x<1时,f(x)-f(1)≥c(x-1)可化为:$\frac{f(x)-f(1)}{x-1}$≤c,则c≥-1,
当x>1时,f(x)-f(1)≥c(x-1)可化为:$\frac{f(x)-f(1)}{x-1}$≥c,则c≤1,
故c∈[-1,1];
②当x0=$\frac{1}{2}$时,f(x)-f(x0)≥c(x-x0)可化为:f(x)-f($\frac{1}{2}$)≥c(x-$\frac{1}{2}$)
当0<x<$\frac{1}{2}$时,f(x)-f($\frac{1}{2}$)≥c(x-$\frac{1}{2}$)可化为:$\frac{f(x)-f(\frac{1}{2})}{x-\frac{1}{2}}$≤c,则c≥f′($\frac{1}{2}$)=-2,
当$\frac{1}{2}$<x<1时,f(x)-f($\frac{1}{2}$)≥c(x-$\frac{1}{2}$)可化为:$\frac{f(x)-f(\frac{1}{2})}{x-\frac{1}{2}}$≥c,则c≤f′($\frac{1}{2}$)=-2,
当x>1时,f(x)-f($\frac{1}{2}$)≥c(x-$\frac{1}{2}$)可化为:$\frac{f(x)-f(\frac{1}{2})}{x-\frac{1}{2}}$≥c,则c≤1,
故c=-2,
故答案为:[-1,1],-2
点评 本题考查的知识点是分段函数的应用,对数函数的图象与性质,导数的几何意义,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
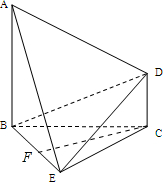 如图,已知AB⊥平面BCE,CD∥AB,△BCE是等边三角形,AB=BC=2CD,F为线段BE的中点.
如图,已知AB⊥平面BCE,CD∥AB,△BCE是等边三角形,AB=BC=2CD,F为线段BE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
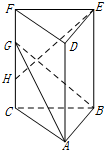 如图所示,在直三棱柱ABC-DEF中,底面ABC的棱AB⊥BC,且AB=BC=2.点G、H在棱CF上,且GH=HG=GF=1
如图所示,在直三棱柱ABC-DEF中,底面ABC的棱AB⊥BC,且AB=BC=2.点G、H在棱CF上,且GH=HG=GF=1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{2}$ | C. | 3$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
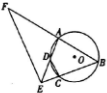 如图,A,B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.
如图,A,B,C,D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正方体AC1的棱长为a,MN分别为BC1和AC上的点,且$\overrightarrow{AN}$=2$\overrightarrow{NC}$,$\overrightarrow{BM}$=2$\overrightarrow{M{C}_{1}}$,则MN的长为( )
如图,正方体AC1的棱长为a,MN分别为BC1和AC上的点,且$\overrightarrow{AN}$=2$\overrightarrow{NC}$,$\overrightarrow{BM}$=2$\overrightarrow{M{C}_{1}}$,则MN的长为( )| A. | a | B. | $\sqrt{2}$a | C. | $\frac{\sqrt{5}}{3}$a | D. | $\frac{\sqrt{6}}{3}$a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com