
分析 (1)求出g(x)的导数,可得切线的斜率和切点,求得切线的方程,再求f(x)的导数,可得l与f(x)图象相切的切点的横坐标,进而得到纵坐标,代入f(x),可得c的值;
(2)设F(x)=f(x)-g(x)=4x-$\frac{2}{1+c}$x2-$\frac{4c}{1+c}$lnx,求出F(x)的导数,对c讨论,分c≤0时,0<c<1,由导数大于0,可得增区间;导数小于0,可得减区间;
(3)c>1时,由f(x)-g(x)在(1,c)递增;在(0,1),(c,+∞)递减.可得x=c取得极大值;x=1处取得极小值,可得h(c)的解析式,可令h(c)=0,化简可得a=2c2-4clnc-2,设m(c)=2c2-4clnc-2,c>1,求得m(c)的导数,可得单调性,对a讨论,分a≤0,a>0,即可得到所求零点的个数.
解答 解:(1)g(x)=$\frac{4c}{1+c}$lnx的导数为g′(x)=$\frac{4c}{1+c}$•$\frac{1}{x}$,
可得g(x)在x=e处的切线的斜率为$\frac{4c}{e(1+c)}$,
切点为(e,$\frac{4c}{1+c}$),
可得切线l的方程为y-$\frac{4c}{1+c}$=$\frac{4c}{e(1+c)}$(x-e),
即为y=$\frac{4c}{e(1+c)}$x,
函数f(x)=4x-$\frac{2}{1+c}$x2的导数为f′(x)=4-$\frac{4}{1+c}$x,
设l与f(x)的切点为(m,n),
则4-$\frac{4}{1+c}$m=$\frac{4c}{e(1+c)}$,解得m=1+c-$\frac{c}{e}$,
则n=$\frac{4c}{e(1+c)}$(1+c-$\frac{c}{e}$),
即有$\frac{4c}{e(1+c)}$(1+c-$\frac{c}{e}$)=4(1+c-$\frac{c}{e}$)-$\frac{2}{1+c}$(1+c-$\frac{c}{e}$)2,
化简可得c=$\frac{e}{1-e}$;
(2)设F(x)=f(x)-g(x)=4x-$\frac{2}{1+c}$x2-$\frac{4c}{1+c}$lnx,
则F′(x)=4-$\frac{4}{1+c}$x-$\frac{4c}{1+c}$•$\frac{1}{x}$
=-4•$\frac{(x-1)(x-c)}{(1+c)x}$,
若c≤0时,由F′(x)>0可得0<x<1;
由F′(x)<0可得x>1;
若0<c<1时,由F′(x)>0可得c<x<1;
由F′(x)<0可得0<x<c或x>1.
综上可得,c≤0时,函数f(x)-g(x)在(0,1)递增;
在(1,+∞)递减;
0<c<1时,函数f(x)-g(x)在(c,1)递增;
在(0,c),(1,+∞)递减;
(3)若c>1时,可得f(x)-g(x)在(1,c)递增;
在(0,1),(c,+∞)递减.
即有f(x)-g(x)的极大值M(c)=4c-$\frac{2}{1+c}$•c2-$\frac{4c}{1+c}$lnc,
极小值N(c)=4-$\frac{2}{1+c}$-$\frac{4c}{1+c}$ln1=$\frac{2+4c}{1+c}$,
则h(c)=M(c)-N(c)-$\frac{a}{c+1}$=$\frac{2{c}^{2}+4c}{1+c}$-$\frac{4c}{1+c}$lnc-$\frac{2+4c}{1+c}$-$\frac{a}{c+1}$,
令h(c)=0,可得a=2c2-4clnc-2,设m(c)=2c2-4clnc-2,c>1,
可得m′(c)=4c-4(1+lnc)=4(c-1-lnc),
由c-1-lnc的导数为1-$\frac{1}{c}$,由c>1可得1-$\frac{1}{c}$>0,即有c-1-lnc>0,
即m′(c)>0,可得m(c)>m(1)=0,
则当a≤0时,a=2c2-4clnc-2无解;
当a>0时,a=2c2-4clnc-2一解.
综上可得,当a≤0时,函数h(c)无零点;
当a>0时,函数h(c)有一个零点.
点评 本题考查导数的运用:求切线的方程和单调区间、极值,考查函数的单调性,注意运用分类讨论的思想方法,考查函数零点的个数问题的解法,注意运用转化思想,构造函数法,考查化简整理的运算能力,属于中档题.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个零点 | B. | 至多有一个零点 | C. | 可能存在2个零点 | D. | 可能存在3个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,$\frac{2π}{3}$) | B. | (4,$\frac{4π}{3}$) | C. | (2,$\frac{2π}{3}$) | D. | (2,$\frac{4π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
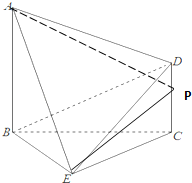 如图:已知平面ABCD⊥平面BCE,平面ABE⊥平面BCE,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形,P是线段CD上的动点.
如图:已知平面ABCD⊥平面BCE,平面ABE⊥平面BCE,AB∥CD,AB=BC=4,CD=2,△BEC为等边三角形,P是线段CD上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com