
分析 (1)由题意可得:$\frac{1}{2}×2c•b$=3,b=c,又a2=b2+c2,联立解出即可得出.
(2)以AB为直径的圆过定点原点O(0,0).下面给出证明分析:①当切线的斜率不存在时,直接解出验证即可得出.
②当切线的斜率存在时,设A(x1,y1),B(x2,y2).设切线的方程为:y=kx+m,利用与圆相切的性质可得:$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\sqrt{2}$,即m2=2(1+k2).(*)把切线方程代入椭圆方程可得:(1+2k2)x2+4kmx+2m2-6=0,利用根与系数的关系、及其(*),只要证明$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=(1+k2)x1x2+km(x1+x2)+m2=0即可得出结论.
解答 解:(1)由题意可得:$\frac{1}{2}×2c•b$=3,b=c,又a2=b2+c2,联立解得:b=c=$\sqrt{3}$,a2=6.
∴椭圆C的方程是$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}$=1.
(2)以AB为直径的圆过定点原点O(0,0).下面给出证明:
①当切线的斜率不存在时,即切线经过点$(±\sqrt{2},0)$时,代入椭圆方程可得:$\frac{2}{6}+\frac{{y}^{2}}{3}=1$,解得y=±$\sqrt{2}$.
不妨取A$(\sqrt{2},\sqrt{2})$,B$(\sqrt{2},-\sqrt{2})$,则$\overrightarrow{OA}•\overrightarrow{OB}$=2-2=0,∴OA⊥OB.
②当切线的斜率存在时,设A(x1,y1),B(x2,y2).
设切线的方程为:y=kx+m,则$\frac{|m|}{\sqrt{1+{k}^{2}}}$=$\sqrt{2}$,即m2=2(1+k2).
代入椭圆方程可得:(1+2k2)x2+4kmx+2m2-6=0,
∴x1+x2=-$\frac{4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-6}{1+2{k}^{2}}$.
y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2.
∴$\overrightarrow{OA}•\overrightarrow{OB}$=x1x2+y1y2=(1+k2)x1x2+km(x1+x2)+m2=$\frac{(2{m}^{2}-6)(1+{k}^{2})}{1+2{k}^{2}}$-$\frac{4{k}^{2}{m}^{2}}{1+2{k}^{2}}$+m2=$\frac{3{m}^{2}-6(1+{k}^{2})}{1+2{k}^{2}}$=$\frac{6(1+{k}^{2})-6(1+{k}^{2})}{1+2{k}^{2}}$=0.
∴$\overrightarrow{OA}⊥\overrightarrow{OB}$,即OA⊥OB.
∴以AB为直径的圆过定点原点O(0,0).
综上①②可得:以AB为直径的圆过定点原点O(0,0).
点评 本题考查了椭圆的标准方程及其性质、直线与圆相切及其直线与椭圆相交问题、一元二次方程的根与系数的关系、向量垂直与数量积的关系,考查了推理能力与计算能力,属于难题.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
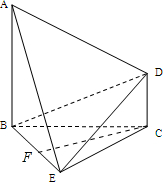 如图,已知AB⊥平面BCE,CD∥AB,△BCE是等边三角形,AB=BC=2CD,F为线段BE的中点.
如图,已知AB⊥平面BCE,CD∥AB,△BCE是等边三角形,AB=BC=2CD,F为线段BE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
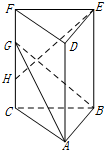 如图所示,在直三棱柱ABC-DEF中,底面ABC的棱AB⊥BC,且AB=BC=2.点G、H在棱CF上,且GH=HG=GF=1
如图所示,在直三棱柱ABC-DEF中,底面ABC的棱AB⊥BC,且AB=BC=2.点G、H在棱CF上,且GH=HG=GF=1查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直线AB经过⊙O上一点C,⊙O的半径为3,△AOB是等腰三角形,且C是AB中点,⊙O交直线OB于E、D.
如图,直线AB经过⊙O上一点C,⊙O的半径为3,△AOB是等腰三角形,且C是AB中点,⊙O交直线OB于E、D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com