
分析 (Ⅰ)由x=ρcosθ,y=ρsinθ,两角和的正弦公式,可得直线l的直角坐标方程;运用同角的平方关系,可得曲线C的普通方程,再由直线和圆相切的条件:d=r,由点到直线的距离公式,可得a的值;
(Ⅱ)设点P(x0,y0)及过点P且与l平行的直线为L1:$\left\{\begin{array}{l}{x={x}_{0}-\frac{\sqrt{2}}{2}t}\\{y={y}_{0}+\frac{\sqrt{2}}{2}t}\end{array}\right.$,(t为参数),代入曲线C的方程,由韦达定理和参数的几何意义,结合条件可得P的轨迹方程,注意条件的限制.
解答 解:(Ⅰ)ρsin(θ+$\frac{π}{4}$)=a,即为ρ($\frac{\sqrt{2}}{2}$sinθ+$\frac{\sqrt{2}}{2}$cosθ)=a,
由x=ρcosθ,y=ρsinθ,
可得直线l的直角坐标方程为$\frac{\sqrt{2}}{2}$x+$\frac{\sqrt{2}}{2}$y=a,
曲线C参数方程为$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$(θ为参数),
由同角的平方关系,消去参数θ,可得曲线C:x2+y2=1,
由C与l有且只有一个公共点,即直线和圆相切,
可得圆心(0,0)到直线的距离为d=$\frac{|0+0+a|}{\sqrt{\frac{1}{2}+\frac{1}{2}}}$=1,
解得a=±1;
(Ⅱ)设点P(x0,y0)及过点P且与l平行的直线为L1:$\left\{\begin{array}{l}{x={x}_{0}-\frac{\sqrt{2}}{2}t}\\{y={y}_{0}+\frac{\sqrt{2}}{2}t}\end{array}\right.$,(t为参数),
由直线L1与曲线C:x2+y2=1相交可得:t2-$\sqrt{2}$(x0+y0)t+x02+y02-1=0,
即有t1t2=x02+y02-1,
因为|PA|•|PB|=3,
所以|x02+y02-1|=3,即x02+y02=4,
联立$\left\{\begin{array}{l}{y=-x+m}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$可得2x2-2mx+m2-1=0,
由△=4m2-4×2(m2-1)>0,解得-$\sqrt{2}$<m<$\sqrt{2}$,
点P的轨迹的直角坐标方程为x2+y2=4(夹在两直线y=-x±$\sqrt{2}$之间的两段圆弧).
点评 本题考查极坐标方程和直角坐标方程的互化、参数方程和普通方程的互化,考查直线和圆的位置关系的判断和应用,考查直线的参数方程的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
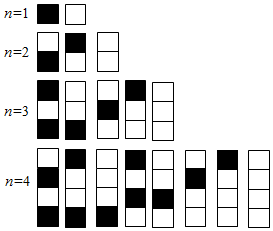 给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示,由此推断,当n=6时,至少有两个黑色正方形相邻的着色方案共有( )种.
给n个自上而下相连的正方形着黑色或白色.当n≤4时,在所有不同的着色方案中,黑色正方形互不相邻的着色方案如图所示,由此推断,当n=6时,至少有两个黑色正方形相邻的着色方案共有( )种.| A. | 21 | B. | 32 | C. | 43 | D. | 54 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com