练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    16．对于数25，规定第1次操作为23+53=133，第2次操作为13+33+33=55，如此反复操作，则第2016次操作后得到的数是250．

    分析 第1次操作为23+53=133，第2次操作为13+33+33=55，第3次操作为53+53=250，第4次操作为23+53+03=133，所以操作结果，以3为周期，循环出现，由此可得第2016次操作后得到的数．

    解答 解：第1次操作为23+53=133，
    第2次操作为13+33+33=55，
    第3次操作为53+53=250，
    第4次操作为23+53+03=133，
    所以操作结果，以3为周期，循环出现，
    由此可得第2016次操作后得到的数与第3次操作后得到的数相同，
    故第2016次操作后得到的数是250，
    故答案为：250．

    点评 本题考查合情推理，考查学生的阅读能力，解题的关键是得出操作结果，以3为周期，循环出现．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    6．已知f（x）=ax-lnx．
    （1）讨论f（x）单调性；
    （2）当a＞0时，已知f（x1）=f（x2），x1≠x2，求证：x1+x2＞$\frac{2}{a}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．设a∈Z，且0＜a＜13，若532016+a能被13整除，则a=（　　）
    A．0B．1C．11D．12

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．图中的三角形称为希尔宾斯基（Sierpinski）三角形．黑色的三角形个数依次构成一个数列，则这个数列的一个通项公式是（　　）
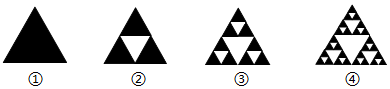
    A．an=3n-1B．an=3nC．an=3n-2nD．an=3n-1+2n-3

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．如图，第1个图形是由正三角形“扩展”而来的，第2个图形是由正方形“扩展”而来的，第3个图形是由正五边形“扩展”而来的，…，第n个图形是由正n+2边形“扩展”而来的（n∈N*）．则在第n个图形中共有（n+2）（n+3）个顶点．（用n表示）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．直线l的极坐标方程为ρsin（θ+$\frac{π}{4}$）=a，曲线C参数方程为$\left\{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}\right.$（θ为参数），已知C与l有且只有一个公共点．
    （Ⅰ）求a的值；
    （Ⅱ）过P点作平行于l的直线交C于A，B两点，且|PA|•|PB|=3，求点P轨迹的直角坐标方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．不等式|$\sqrt{x-1}$-2|＞1的解集是{x|1≤x＜2或x＞10}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．“推迟退休”问题备受关注，调查机构对某小区的位居民进行了调查，得到如表的列联表：
    支持推迟退休不支持推迟退休合计
    年龄不大于45岁206080
    年龄大于45岁101020
    合计3070100
    （1）请画出列联表的等高条形图，并通过图形判断两个分类变量是否有关系．
    （2）根据表中数据，判断是否有95%的把握认为“不同年龄的居民在是否支持推迟退休上观点有差异”？
    （3）已知在被调查的支持推迟退休且年龄大于45 岁的居民中有5 位男性，其中2 位是一线工人，现从这5 位男性中随机抽取3 人，求至多有1 位一线工人的概率
    附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，n=a+b+c+d
    P（K2＞k）0.1000.0500.0250.010
    k2.7063.8415.0246.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．函数y=$\sqrt{-lg（1-x）}$的定义域为[0，1）．

    查看答案和解析>>

    同步练习册答案