
| 支持推迟退休 | 不支持推迟退休 | 合计 | |
| 年龄不大于45岁 | 20 | 60 | 80 |
| 年龄大于45岁 | 10 | 10 | 20 |
| 合计 | 30 | 70 | 100 |
| P(K2>k) | 0.100 | 0.050 | 0.025 | 0.010 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
分析 (1)根据列联表即可画出等高条形图,由图形可判断两个分类变量是有关系;
(2)根据所给的2×2列联表得到求观测值所用的数据,把数据代入观测值公式中,求出观测值,同所给的临界值表进行比较,即可得到结果.
(3)根据概率公式,分别求得5个人中由一个一线工人及没有一线工人的事件个数,即可求得至多有1 位一线工人的概率.
解答 解:(1)列联表的等高条形图: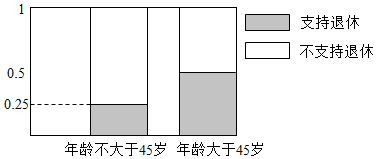
由图形可判断两个分类变量是有关系;
(2)将2×2列联表的数据代入公式得K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$=$\frac{100×(20×10-60×10)^{2}}{80×20×30×70}$≈4.762>3.841,
所以由95%的把握认为“不同年龄的居民在是否支持推迟退休上观点有差异”;
(3)记“5位男性中随机抽取3 人,求至多有1 位一线工人”的事件为A,
P(A)=$\frac{{C}_{2}^{1}•{C}_{3}^{2}}{{C}_{5}^{3}}$+$\frac{{C}_{3}^{3}}{{C}_{5}^{3}}$=$\frac{7}{10}$,
5位男性中随机抽取3 人,求至多有1 位一线工人的概率$\frac{7}{10}$.
点评 本题考查独立性检验的应用、古典概型及计算公式,考查计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
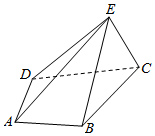 在如图所示的四棱锥E-ABCD中,底面ABCD为直角梯形,AB⊥AD,CD⊥AD,且AB=AD=$\frac{1}{2}$CD=2,侧面BEC为正三角形,且平面BEC⊥平面ABCD.
在如图所示的四棱锥E-ABCD中,底面ABCD为直角梯形,AB⊥AD,CD⊥AD,且AB=AD=$\frac{1}{2}$CD=2,侧面BEC为正三角形,且平面BEC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [0,1) | C. | [-9,+∞) | D. | [-9,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个零点 | B. | 至多有一个零点 | C. | 可能存在2个零点 | D. | 可能存在3个零点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com