
分析 由题意画出图形,求出A,B的坐标,设出P的坐标,写出AP,BP所在直线方程,求出M,N的坐标,由$\overrightarrow{FM}•\overrightarrow{FN}=0$可得∠MFN=90°.
解答 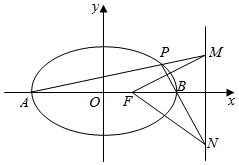 解:如图A(-a,0),B(a,0),设P(x0,y0),
解:如图A(-a,0),B(a,0),设P(x0,y0),
则${k}_{PA}=\frac{{y}_{0}}{{x}_{0}+a}$,直线PA:$y=\frac{{y}_{0}}{{x}_{0}+a}(x+a)$,
∴M($\frac{{a}^{2}}{c},\frac{a{y}_{0}(a+c)}{c({x}_{0}+a)}$),
${k}_{PB}=\frac{{y}_{0}}{{x}_{0}-a}$,直线PB:$y=\frac{{y}_{0}}{{x}_{0}-a}(x-a)$,
∴N($\frac{{a}^{2}}{c},\frac{a{y}_{0}(a-c)}{c({x}_{0}-a)}$).
则$\overrightarrow{FM}=(\frac{a{y}_{0}(a+c)}{c({x}_{0}+a)},\frac{{b}^{2}}{c})$,$\overrightarrow{FN}=(\frac{a{y}_{0}(a-c)}{c({x}_{0}-a)},\frac{{b}^{2}}{c})$,
∵$\overrightarrow{FM}•\overrightarrow{FN}=\frac{{a}^{2}{{y}_{0}}^{2}{b}^{2}}{{c}^{2}({{x}_{0}}^{2}-{a}^{2})}+\frac{{b}^{4}}{{c}^{2}}$=$\frac{{a}^{2}{b}^{2}}{{c}^{2}}(-\frac{{b}^{2}}{{a}^{2}})+\frac{{b}^{4}}{{c}^{2}}=0$.
∴$\overrightarrow{FM}⊥\overrightarrow{FN}$,即∠MFN=90°.
故答案为:90°.
点评 本题考查了直线与圆锥曲线的关系,考查了数形结合的解题思想方法与数学转化思想方法,考查了学生综合处理问题解决问题的能力,考查了学生的运算能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持推迟退休 | 不支持推迟退休 | 合计 | |
| 年龄不大于45岁 | 20 | 60 | 80 |
| 年龄大于45岁 | 10 | 10 | 20 |
| 合计 | 30 | 70 | 100 |
| P(K2>k) | 0.100 | 0.050 | 0.025 | 0.010 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com