
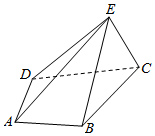
 在如图所示的四棱锥E-ABCD中,底面ABCD为直角梯形,AB⊥AD,CD⊥AD,且AB=AD=$\frac{1}{2}$CD=2,侧面BEC为正三角形,且平面BEC⊥平面ABCD.
在如图所示的四棱锥E-ABCD中,底面ABCD为直角梯形,AB⊥AD,CD⊥AD,且AB=AD=$\frac{1}{2}$CD=2,侧面BEC为正三角形,且平面BEC⊥平面ABCD.分析 (1)CD的中点F,使得BC∥平面AEF,利用已知条件结合线面平行的判定即可证明;
(2)取BC中点O,由侧面BEC为正三角形,得EO⊥BC,又平面BEC⊥平面ABCD,可得EO⊥平面ABCD,在平面ABCD内,过O作Ox∥AB,作Oy⊥AB,建立如图所示空间直角坐标系,利用$\overrightarrow{EA}$与平面BEC的法向量所成角的余弦值可得直线AE与平面BEC所成角的正弦值.
解答  解:(1)如图,CD的中点F,使得BC∥平面AEF.
解:(1)如图,CD的中点F,使得BC∥平面AEF.
事实上:∵底面ABCD为直角梯形,且AB⊥AD,CD⊥AD,
∴AB∥CD,又AB=$\frac{1}{2}$CD,
∴取CD中点F,连接AF,EF,则AB=FC,
∴四边形ABCF为平行四边形,则BC∥AF,
又AF?平面AEF,BC?平面AEF,
∴BC∥平面AEF;
(2)取BC中点O,∵侧面BEC为正三角形,
∴EO⊥BC,又平面BEC⊥平面ABCD,
∴EO⊥平面ABCD,
在平面ABCD内,过O作Ox∥AB,作Oy⊥AB,建立如图所示空间直角坐标系.
∵AB=AD=$\frac{1}{2}$CD=2,∴BC=$2\sqrt{2}$,则OE=$\sqrt{6}$,
∴O(0,0,0),E(0,0,$\sqrt{6}$),B(1,1,0),A(3,1,0).
则$\overrightarrow{EA}=(3,1,-\sqrt{6})$,$\overrightarrow{OE}=(0,0,\sqrt{6})$,$\overrightarrow{OB}=(1,1,0)$.
设平面BEC的一个法向量为$\overrightarrow{n}=(x,y,z)$,
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{OB}=0}\\{\overrightarrow{n}•\overrightarrow{OE}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{x+y=0}\\{\sqrt{6}z=0}\end{array}\right.$,取y=-1,则x=1.
∴$\overrightarrow{n}=(1,-1,0)$.
设直线AE与平面BEC所成角为θ,
则sinθ=|cos<$\overrightarrow{EA},\overrightarrow{n}$>|=|$\frac{\overrightarrow{EA}•\overrightarrow{n}}{|\overrightarrow{EA}||\overrightarrow{n}|}$|=|$\frac{3×1-1×1}{\sqrt{{3}^{2}+{1}^{2}+(-\sqrt{6})^{2}}•\sqrt{2}}$|=$\frac{\sqrt{2}}{4}$.
点评 本题考查直线与平面平行的判定,考查空间想象能力和思维能力,训练了利用空间向量求解线面角问题,是中档题.


科目:高中数学 来源: 题型:解答题
| 支持推迟退休 | 不支持推迟退休 | 合计 | |
| 年龄不大于45岁 | 20 | 60 | 80 |
| 年龄大于45岁 | 10 | 10 | 20 |
| 合计 | 30 | 70 | 100 |
| P(K2>k) | 0.100 | 0.050 | 0.025 | 0.010 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com