
分析 (1)求出圆的圆心,代入直线方程,求出直线的斜率,即可求直线l的方程;
(2)利用倾斜角求出直线的斜率,然后求出直线的方程,利用点到直线的距离,半径,半弦长的关系求弦长AB.
解答 解:(1)圆C:x2+(y-1)2=9的圆心为C(0,1),直线过点P、C,
所以直线l的斜率为k=$\frac{2-1}{\sqrt{3}-0}$=$\frac{\sqrt{3}}{3}$,
直线l的方程为y=$\frac{\sqrt{3}}{3}$x+1,即$\sqrt{3}$x-3y-3=0;
(2)当直线l的倾斜角为$\frac{π}{3}$时,斜率为k=tan$\frac{π}{3}$=$\sqrt{3}$,
直线l的方程为y-2=$\sqrt{3}$(x-$\sqrt{3}$),即$\sqrt{3}$x-y-1=0;
又圆心C(0,1)到直线l的距离为d=$\frac{|\sqrt{3}×0-1×1-1|}{\sqrt{{(\sqrt{3})}^{2}{+(-1)}^{2}}}$=1,圆的半径为r=3,
所以弦AB的长为|AB|=2$\sqrt{{r}^{2}{-d}^{2}}$=2×$\sqrt{{3}^{2}{-1}^{2}}$=4$\sqrt{2}$.
点评 本题考查了直线与圆的位置关系与应用问题,也考查了直线的斜率与点到直线的距离的计算问题,是基础题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 支持推迟退休 | 不支持推迟退休 | 合计 | |
| 年龄不大于45岁 | 20 | 60 | 80 |
| 年龄大于45岁 | 10 | 10 | 20 |
| 合计 | 30 | 70 | 100 |
| P(K2>k) | 0.100 | 0.050 | 0.025 | 0.010 |
| k | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
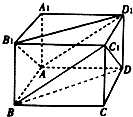 在长方体ABCD-A1B1C1D1中,AB=BC=2AA1=4.
在长方体ABCD-A1B1C1D1中,AB=BC=2AA1=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com