
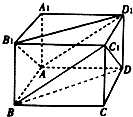
 在长方体ABCD-A1B1C1D1中,AB=BC=2AA1=4.
在长方体ABCD-A1B1C1D1中,AB=BC=2AA1=4.分析 (1)通过证明线面平行,证明平面BDC1∥平面AB1D1;
(2)利用等体积法,求点C1到平面AB1D1的距离.
解答 证明:(1)在长方体ABCD-A1B1C1D1中,B1C1∥AD且B1C1=AD,
∴B1C1DA是平行四边形,
∴C1D∥B1A,
∵B1A?平面AB1D1,C1D?平面AB1D1,
∴C1D∥平面AB1D1,
同理BD∥平面AB1D1,
∵C1D∩BD=D,
∴平面BDC1∥平面AB1D1;
解:(2)设点C1到平面AB1D1的距离为h.
∵AB1=AD1=2$\sqrt{5}$,B1D1=4$\sqrt{2}$,
∴由${V}_{{C}_{1}-A{B}_{1}{D}_{1}}$=${V}_{A-{B}_{1}{C}_{1}{D}_{1}}$得$\frac{1}{3}×\frac{1}{2}×4\sqrt{2}×2\sqrt{3}h$=$\frac{1}{3}×\frac{1}{2}×4×4×2$,
∴h=$\frac{2\sqrt{6}}{3}$,
∴点C1到平面AB1D1的距离为$\frac{2\sqrt{6}}{3}$.
点评 本题考查线面平行、平面与平面平行的判定,考查点到平面的距离的计算,正确运用等体积是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
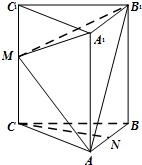 如图,在正三棱ABC-A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M、N分别是CC1、AB的中点
如图,在正三棱ABC-A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M、N分别是CC1、AB的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.01的前提下认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.01的前提下认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过0.001的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过0.001的前提下,认为“爱好该项运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少有一个零点 | B. | 至多有一个零点 | C. | 可能存在2个零点 | D. | 可能存在3个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正三棱柱ABC-A1B1C1,各棱长都是2,M是AC中点.
如图,正三棱柱ABC-A1B1C1,各棱长都是2,M是AC中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com