
| �� | Ů | �ܼ� | |
| ���� | 40 | 20 | 60 |
| ������ | 20 | 30 | 50 |
| �ܼ� | 60 | 50 | 110 |
| P��K2��k�� | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A�� | �ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ�����ø����˶����Ա��йء� | |
| B�� | �ڷ�����ĸ��ʲ�����0.01��ǰ������Ϊ�����ø����˶����Ա��ء� | |
| C�� | �ڷ�����ĸ��ʲ�����0.001��ǰ���£���Ϊ�����ø����˶����Ա��йء� | |
| D�� | �ڷ�����ĸ��ʲ�����0.001��ǰ���£���Ϊ�����ø����˶����Ա��ء� |
 ��������������������ϵ�д�
��������������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����ֵ��Ϊ[1����] | B�� | �˺��������� | C�� | �˺���Ϊż���� | D�� | ����f[f��x��]=x������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
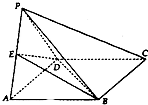 ��ͼ����PAD��������ABCD����һ��AD��ƽ��PAD��ƽ��ABCD������PA=PD��AB=2����E����PA���е㣮
��ͼ����PAD��������ABCD����һ��AD��ƽ��PAD��ƽ��ABCD������PA=PD��AB=2����E����PA���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
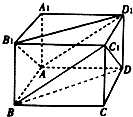 �ڳ�����ABCD-A1B1C1D1�У�AB=BC=2AA1=4��
�ڳ�����ABCD-A1B1C1D1�У�AB=BC=2AA1=4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����ֱ������ABC-A1B1C1�У�BC=AC��AB=$\sqrt{2}$AA1��AC1��A1B��M��N�ֱ���A1B1��AB���е㣬�������н��ۣ�
��ͼ��ʾ����ֱ������ABC-A1B1C1�У�BC=AC��AB=$\sqrt{2}$AA1��AC1��A1B��M��N�ֱ���A1B1��AB���е㣬�������н��ۣ�| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-��=0 | B�� | ��+��=0 | C�� | 2��-��=0 | D�� | 2��+��=0 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com