
 如图所示,在直三棱柱ABC-A1B1C1中,BC=AC,AB=$\sqrt{2}$AA1,AC1⊥A1B,M,N分别是A1B1,AB的中点,给出下列结论:
如图所示,在直三棱柱ABC-A1B1C1中,BC=AC,AB=$\sqrt{2}$AA1,AC1⊥A1B,M,N分别是A1B1,AB的中点,给出下列结论:| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 先证明AM⊥A1B,AM∥NB1,即可得解A1B⊥NB1,又AC1⊥A1B,进而可证平面AMC1⊥平面CBA1,利用面面垂直的性质可证C1M⊥平面A1ABB.
解答  解:∵由已知,设AA1=1,则可求:A1M=$\frac{\sqrt{2}}{2}$,AM=$\sqrt{{A}_{1}{A}^{2}+{A}_{1}{M}^{2}}$=$\frac{\sqrt{3}}{\sqrt{2}}$;
解:∵由已知,设AA1=1,则可求:A1M=$\frac{\sqrt{2}}{2}$,AM=$\sqrt{{A}_{1}{A}^{2}+{A}_{1}{M}^{2}}$=$\frac{\sqrt{3}}{\sqrt{2}}$;
AB=$\sqrt{2}$,A1B=$\sqrt{{A}_{1}{A}^{2}+A{B}^{2}}$=$\sqrt{3}$,
∴sin∠A1AM=$\frac{1}{\sqrt{3}}$,cos∠A1AM=$\frac{\sqrt{2}}{\sqrt{3}}$,sin∠AA1B=$\frac{\sqrt{2}}{\sqrt{3}}$,cos∠AA1B=$\frac{1}{\sqrt{3}}$,
∴设A1B与AM交于点Q点,则:
sin∠A1QA=sin[π-(∠AA1B+∠A1AM)]=sin(∠AA1B+∠A1AM)=sin∠AA1Bcos∠A1AM+cos∠AA1Bsin∠A1AM=$\frac{\sqrt{2}}{\sqrt{3}}×\frac{\sqrt{2}}{\sqrt{3}}$+$\frac{1}{\sqrt{3}}×\frac{1}{\sqrt{3}}$=1,
∴A1B⊥AM.
∵MB1$\stackrel{∥}{=}$AN,
∴四边形ANB1M为平行四边形,可证:AM∥NB1,
可得:A1B⊥NB1,故②正确;
又AC1⊥A1B,所以A1B⊥平面AMC1,所以,平面AMC1⊥平面CBA1,故③正确;
显然有C1M⊥平面A1ABB.故①正确;
故选:D.
点评 本题主要考查了直线与平面垂直的判定,平面与平面垂直的判定和性质,考查了空间想象能力和推理论证能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 28 | C. | 29 | D. | 47 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.01的前提下认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.01的前提下认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过0.001的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过0.001的前提下,认为“爱好该项运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
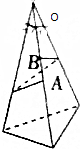 如图,在以O为顶点的三棱锥中,过O的三条棱两两相交都是30°,在一条棱上取A、B两点,OA=4cm,OB=3cm,以A、B为端点用一条绳子紧绕三棱锥的侧面一周(绳和侧面无摩擦),求此绳在A、B两点间的最短绳长.
如图,在以O为顶点的三棱锥中,过O的三条棱两两相交都是30°,在一条棱上取A、B两点,OA=4cm,OB=3cm,以A、B为端点用一条绳子紧绕三棱锥的侧面一周(绳和侧面无摩擦),求此绳在A、B两点间的最短绳长.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com