
分析 以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出二面角B-PC-D的余弦值.
解答 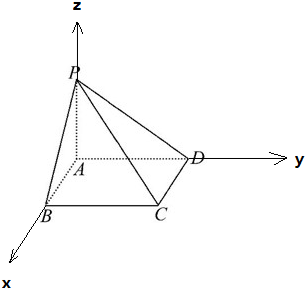 解:如图,以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
解:如图,以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,
B(a,0,0),C(a,2a,0),D(0,2a,0),P(0,0,a),
$\overrightarrow{PB}$=(a,0,-a),$\overrightarrow{PC}$=(a,2a,-a),$\overrightarrow{PD}$=(0,2a,-a),
设平面PBC的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PB}=ax-az=0}\\{\overrightarrow{n}•\overrightarrow{PC}=ax+2ay-az=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,0,1),
设平面PCD的法向量$\overrightarrow{m}$=(x1,y1,z1),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PC}=a{x}_{1}+2a{y}_{1}-a{z}_{1}=0}\\{\overrightarrow{m}•\overrightarrow{PD}=2a{y}_{1}-a{z}_{1}=0}\end{array}\right.$,取y1=1,得$\overrightarrow{m}$=(0,1,2),
设二面角B-PC-D的平面角为θ,由图形知θ为钝角,
则cosθ=-$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=-$\frac{2}{\sqrt{2}•\sqrt{5}}$=-$\frac{\sqrt{10}}{5}$.
∴二面角B-PC-D的余弦值为-$\frac{\sqrt{10}}{5}$.
点评 本题考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:解答题
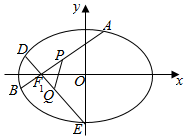 已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,点M(1,$\frac{{\sqrt{2}}}{2}}$)在椭圆C上.
已知椭圆C:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,点M(1,$\frac{{\sqrt{2}}}{2}}$)在椭圆C上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 28 | C. | 29 | D. | 47 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | (-∞,-$\sqrt{2}$]∪[$\sqrt{2}$,+∞) | C. | (1,$\sqrt{2}$) | D. | [1,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
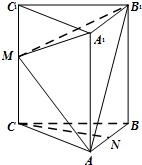 如图,在正三棱ABC-A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M、N分别是CC1、AB的中点
如图,在正三棱ABC-A1B1C1(侧棱垂直于底面,且底面是正三角形)中,AC=CC1=6,M、N分别是CC1、AB的中点查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.01的前提下认为“爱好该项运动与性别有关” | |
| B. | 在犯错误的概率不超过0.01的前提下认为“爱好该项运动与性别无关” | |
| C. | 在犯错误的概率不超过0.001的前提下,认为“爱好该项运动与性别有关” | |
| D. | 在犯错误的概率不超过0.001的前提下,认为“爱好该项运动与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
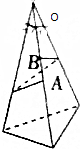 如图,在以O为顶点的三棱锥中,过O的三条棱两两相交都是30°,在一条棱上取A、B两点,OA=4cm,OB=3cm,以A、B为端点用一条绳子紧绕三棱锥的侧面一周(绳和侧面无摩擦),求此绳在A、B两点间的最短绳长.
如图,在以O为顶点的三棱锥中,过O的三条棱两两相交都是30°,在一条棱上取A、B两点,OA=4cm,OB=3cm,以A、B为端点用一条绳子紧绕三棱锥的侧面一周(绳和侧面无摩擦),求此绳在A、B两点间的最短绳长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com