
| A. | [-$\sqrt{2}$,$\sqrt{2}$] | B. | (-∞,-$\sqrt{2}$]∪[$\sqrt{2}$,+∞) | C. | (1,$\sqrt{2}$) | D. | [1,$\sqrt{2}$) |
分析 y=$\sqrt{1-{x}^{2}}$表示的曲线为圆心在原点,半径是1的圆在x轴以及x轴上方的部分,把斜率是1的直线平行移动,即可求得结论.
解答 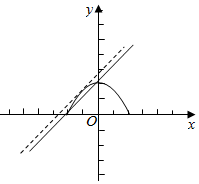 解:∵y=$\sqrt{1-{x}^{2}}$有表示的曲线为圆心在原点,
解:∵y=$\sqrt{1-{x}^{2}}$有表示的曲线为圆心在原点,
半径是1的圆在x轴以及x轴上方的部分.
作出曲线y=$\sqrt{1-{x}^{2}}$有的图象,在同一坐标系中,
再作出直线y=x+m,平移过程中,直线先与圆相切,
再与圆有两个交点,
直线与曲线相切时,可得,$\frac{|m|}{\sqrt{2}}$=1
∴m=$\sqrt{2}$,当直线y=x+m经过点(-1,0)时,m=1,
直线y=x+1,而该直线也经过(0,1),
即直线y=x+1与半圆有2个交点.
m∈[1,$\sqrt{2}$).
故选:D.
点评 本题考查直线与曲线的交点问题,在同一坐标系中,分别作出函数的图象,借助于数形结合是求解的关键.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
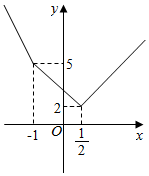 已知函数f(x)=|2x-1|+|x-a|,g(x)=x-1.
已知函数f(x)=|2x-1|+|x-a|,g(x)=x-1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数值域为[1,π] | B. | 此函数不单调 | C. | 此函数为偶函数 | D. | 方程f[f(x)]=x有两解 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
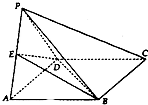 如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点.
如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com