
���� ��1���ٶԶ���ʽ������չ��ʽ���߶�x����������õ����ʽ��
�ڶԢ٣���x=1��n=10���ɺ��ʽ���㼴�ɵõ�����ֵ��
��2���Ԣ��е�x ��ֵ-1�������õ����ʽ$\sum_{k=1}^{n}$��-1��kk${C}_{n}^{k}$=0���Զ���ʽ�Ķ��������߶�x�������ٶԵõ��ĵ�ʽ��x������������x��ֵ-1����ɵ�$\sum_{k=1}^{n}$��-1��kk2${C}_{n}^{k}$=0����Ӽ��ɵõ����� $\sum_{k=1}^n$��-1��kk��k+1��Cnk��
��� �⣺��1����֤������ʽ��1+x��n=Cn0+Cn1x+��+Cnn-1xn-1+Cnnxn��x��R��������n��2����
���߶�x���ɵ�
n��1+x��n-1=Cn1+2${C}_{n}^{2}$x+��+��n-1��Cnn-1xn-2+nCnnxn-1��
����n[��1+x��n-1-1]=2${C}_{n}^{2}$x+��+��n-1��Cnn-1xn-2+nCnnxn-1=$\sum_{k=2}^n$k$C_n^k$xk-1��
���ɢ���x=1�ɵã�n��2n-1-1��=$\sum_{k=2}^n$k$C_n^k$��
�ɵã�C101+2C102+3C103+��+10C1010=10+10��29-1��=5120��
��2���ڢ�ʽ�У���x=-1���ɵ�n[��1-1��n-1-1]=$\sum_{k=2}^n$k$C_n^k$��-1��k-1��
������$\sum_{k=1}^{n}$��-1��k-1k${C}_{n}^{k}$=0��
����$\sum_{k=1}^{n}$��-1��kk${C}_{n}^{k}$=0��
��n��1+x��n-1=Cn1+2Cn2x+��+��n-1��Cnn-1xn-2+nCnnxn-1��n��3��
���߶�x����n��n-1����1+x��n-2=2Cn2+3•2Cn3x+��+n��n-1��Cnnxn-2
����ʽ�У���x=-1����0=2Cn2+3•2Cn3��-1��+��+n��n-1��Cn2��-1��n-2
��$\sum_{k=2}^{n}$k��k-1��${C}_{n}^{k}$��-1��k-2=0��
�༴$\sum_{k=2}^{n}$��k2-k��${C}_{n}^{k}$��-1��k=0��
��$\sum_{k=1}^{n}$��-1��kk${C}_{n}^{k}$=0��
��ʽ��ӿɵã�$\sum_{k=1}^{n}$��-1��kk2${C}_{n}^{k}$=0��
���Ͽɵã�$\sum_{k=1}^n$��-1��kk��k+1��Cnk=$\sum_{k=1}^{n}$��-1��kk2${C}_{n}^{k}$+$\sum_{k=1}^{n}$��-1��kk${C}_{n}^{k}$=0��
���� ���⿼�鵼���ĸ����Ӧ�ã�ע��Ե�ʽ�������������ʽ���������ã�ע�����ø�ֵ�������黯�������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-$\sqrt{2}$��$\sqrt{2}$] | B�� | ��-�ޣ�-$\sqrt{2}$]��[$\sqrt{2}$��+�ޣ� | C�� | ��1��$\sqrt{2}$�� | D�� | [1��$\sqrt{2}$�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ��Բ | B�� | ��������һ��Բ | ||
| C�� | ����ֱ�� | D�� | һ������һ��Բ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
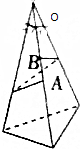 ��ͼ������OΪ����������У���O�������������ཻ����30�㣬��һ������ȡA��B���㣬OA=4cm��OB=3cm����A��BΪ�˵���һ�����ӽ��������IJ���һ�ܣ����Ͳ�����Ħ�������������A��B���������������
��ͼ������OΪ����������У���O�������������ཻ����30�㣬��һ������ȡA��B���㣬OA=4cm��OB=3cm����A��BΪ�˵���һ�����ӽ��������IJ���һ�ܣ����Ͳ�����Ħ�������������A��B����������������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{6}}{6}$ | B�� | $\frac{\sqrt{3}}{3}$ | C�� | $\frac{\sqrt{2}}{2}$ | D�� | $\frac{\sqrt{6}}{3}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com