
分析 (1)利用绝对值三角不等式求得y的最小值,从而求得a的范围.
(2)由a≥3,及均值不等式求得g(a)的最小值.
解答 (1)设y=|x-2|+|x+1|,由绝对值的性质可知:y=|x-2|+|x+1|≥|(x-2)-(x+1)|=3,
∴函数y=|x-2|+|x+1|的值域是y≥3,
要使方程|x-2|+|x+1|=a有解,a≥y最小值 ,
∴a的取值范围是:a≥3.
(2)由a≥3,及均值不等式,可知$g(a)=a+\frac{32}{a^2}=\frac{a}{2}+\frac{a}{2}+\frac{32}{a^2}≥3\root{3}{{\frac{a}{2}×\frac{a}{2}×\frac{32}{a^2}}}=6$,
当且仅当$\frac{a}{2}=\frac{32}{a^2}$时取等号,此时,a=4∈(3,+∞),
∴$g(a)=a+\frac{32}{a^2}$的最小值等于6.
点评 本题主要考查绝对值的意义,绝对值不等式的解法,体现了转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
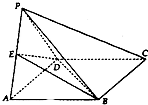 如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点.
如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,l1,l2,l3是同一平面内的三条平行直线,l2,l3在l1的同侧.l1与l2的距离是d,l2与l3的距离是2d,边长为1的正三角形ABC的三个顶点分别在l1,l2,l3上,则d=$\frac{{\sqrt{21}}}{14}$.
如图,l1,l2,l3是同一平面内的三条平行直线,l2,l3在l1的同侧.l1与l2的距离是d,l2与l3的距离是2d,边长为1的正三角形ABC的三个顶点分别在l1,l2,l3上,则d=$\frac{{\sqrt{21}}}{14}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 9 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | λ-μ=0 | B. | λ+μ=0 | C. | 2λ-μ=0 | D. | 2λ+μ=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 以三个向量所在线段为棱一定可以作一个平行六面体 | |
| B. | 设平行六面体的三条棱为$\overrightarrow{AB}$,$\overrightarrow{A{A}_{1}}$,$\overrightarrow{AD}$所在线段,则这一平行六面体的体对角线所对应的向量是$\overrightarrow{AB}$+$\overrightarrow{A{A}_{1}}$+$\overrightarrow{AD}$ | |
| C. | 若$\overrightarrow{OP}$=$\frac{1}{2}$($\overrightarrow{PA}$+$\overrightarrow{PB}$)成立,则点P一定是线段AB的中点 | |
| D. | 在空间中,若$\overrightarrow{AB}$与$\overrightarrow{CD}$是共线向量,则A,B,C,D四点共面 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
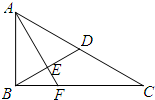 如图,△ABC中,∠ABC=90°,∠C=30°,AB=1,D为AC中点,AE⊥BD于点E,延长AE交BC于点F,沿BD将△ABC折成四面体A-BCD.
如图,△ABC中,∠ABC=90°,∠C=30°,AB=1,D为AC中点,AE⊥BD于点E,延长AE交BC于点F,沿BD将△ABC折成四面体A-BCD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com