
 如图,l1,l2,l3是同一平面内的三条平行直线,l2,l3在l1的同侧.l1与l2的距离是d,l2与l3的距离是2d,边长为1的正三角形ABC的三个顶点分别在l1,l2,l3上,则d=$\frac{{\sqrt{21}}}{14}$.
如图,l1,l2,l3是同一平面内的三条平行直线,l2,l3在l1的同侧.l1与l2的距离是d,l2与l3的距离是2d,边长为1的正三角形ABC的三个顶点分别在l1,l2,l3上,则d=$\frac{{\sqrt{21}}}{14}$. 分析 过A,C作AE,CF垂直于L2,点E,F是垂足,将Rt△BCF绕点B逆时针旋转60°至Rt△BAD处,延长DA交L2于点G,由此可得结论.
解答 解:如图,过A,C作AE,CF垂直于L2,点E,F是垂足,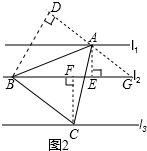
将Rt△BCF绕点B逆时针旋转60°至Rt△BAD处,延长DA交L2于点G.
由作图可知:∠DBG=60°,AD=CF=2d.
在Rt△BDG中,∠BGD=30°.在Rt△AEG中,∠EAG=60°,AE=d,AG=2d,DG=4d.
∴BD=$\frac{4\sqrt{3}}{3}$d
在Rt△ABD中,AB=$\frac{2\sqrt{21}}{3}$d=1,
∴d=$\frac{{\sqrt{21}}}{14}$.
故答案为:$\frac{{\sqrt{21}}}{14}$.
点评 本题考查平行线的性质,等腰三角形,直角三角形的性质,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2] | B. | (-∞,-2) | C. | (-∞,-6] | D. | (-∞,-6) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (1,+∞) | C. | [2,+∞) | D. | [1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)<f(0)<f(4) | B. | f(-1)<f(4)<f(0) | C. | f(0)<f(-1)<f(4) | D. | f(0)<f(4)<f(-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com