练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．函数f（x）=x2+bx+c的两个零点关于x=1对称，则（　　）
    A．f（-1）＜f（0）＜f（4）B．f（-1）＜f（4）＜f（0）C．f（0）＜f（-1）＜f（4）D．f（0）＜f（4）＜f（-1）

    分析 利用二次函数的性质，判断对称轴以及开口方向，然后判断函数值的大小．

    解答 解：函数f（x）=x2+bx+c的开口向上，对称轴为x=1，
    所以f（-1）＞f（0），f（4）=f（-2）＞f（-1）．
    所以f（0）＜f（-1）＜f（4）．
    故选：C．

    点评 本题考查二次函数的性质的应用，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    10．如图，l1，l2，l3是同一平面内的三条平行直线，l2，l3在l1的同侧．l1与l2的距离是d，l2与l3的距离是2d，边长为1的正三角形ABC的三个顶点分别在l1，l2，l3上，则d=$\frac{{\sqrt{21}}}{14}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．平面直角坐标系中有A（0，1），B（2，1），C（3，4），D（-1，2）两点
    （1）求证：A，B，C，D四点共面；
    （2）记（1）中的圆的圆心为M，直线l：2x-y-2=0与圆M相交于点P、Q，求弦长PQ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．下列说法正确的是（　　）
    A．以三个向量所在线段为棱一定可以作一个平行六面体
    B．设平行六面体的三条棱为$\overrightarrow{AB}$，$\overrightarrow{A{A}_{1}}$，$\overrightarrow{AD}$所在线段，则这一平行六面体的体对角线所对应的向量是$\overrightarrow{AB}$+$\overrightarrow{A{A}_{1}}$+$\overrightarrow{AD}$
    C．若$\overrightarrow{OP}$=$\frac{1}{2}$（$\overrightarrow{PA}$+$\overrightarrow{PB}$）成立，则点P一定是线段AB的中点
    D．在空间中，若$\overrightarrow{AB}$与$\overrightarrow{CD}$是共线向量，则A，B，C，D四点共面

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．已知两条直线l1：y=m和l2：y=$\frac{8}{2m+1}$（m＞0），l1与函数y=|log2x|的图象从左到右相交于A、B，l2与函数y=|log2x|的图象从左到右相交于C、D，记线段AC和BD在x轴上的投影长度分别为a，b，当m变化时，$\frac{b}{a}$的最小值为（　　）
    A．16$\sqrt{2}$B．8$\sqrt{2}$C．8$\root{3}{4}$D．4$\root{3}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．如图，在三棱锥P-ABC中，PC⊥底面ABC，AB⊥BC，D是PC的中点．
    （1）求证：平面ABD⊥平面PBC；
    （2）若PA与平面ABC所成的角为30°，AB=BC，求二面角D-AB-C的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．若二面角α-l-β的平面角为θ，a，β的法向量分别为$\overrightarrow{m}$，$\overrightarrow{n}$，则cosθ等于（　　）
    A．$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$B．$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}•\overrightarrow{n}|}$C．-$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{|\overrightarrow{m}||\overrightarrow{n}|}$D．以上都不对

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

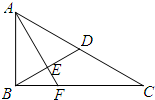    5．如图，△ABC中，∠ABC=90°，∠C=30°，AB=1，D为AC中点，AE⊥BD于点E，延长AE交BC于点F，沿BD将△ABC折成四面体A-BCD．
    （Ⅰ）若M是FC的中点，求证：DM∥平面AEF；
    （Ⅱ）若cos∠AEF=$\frac{1}{3}$，求点D到平面ABC的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知曲线f（x）=x3-2x．求：
    （1）在点（1，-1）处的切线方程；
    （2）过点（1，-1）的切线方程．

    查看答案和解析>>

    同步练习册答案