
| A. | 16$\sqrt{2}$ | B. | 8$\sqrt{2}$ | C. | 8$\root{3}{4}$ | D. | 4$\root{3}{4}$ |
分析 设A,B,C,D各点的横坐标,依题意和对数的运算求横坐标的表达式,由平行投影的概念表示出a和b,代入$\frac{b}{a}$利用指数的运算化简,由m的范围和基本不等式求出最小值.
解答 解:设A,B,C,D各点的横坐标分别为xA,xB,xC,xD,
则-log2xA=m,log2xB=m;-log2xC=$\frac{8}{2m+1}$,log2xD=$\frac{8}{2m+1}$;
∴xA=2-m,xB=2m,xC=${2}^{-\frac{8}{2m+1}}$,xD=${2}^{\frac{8}{2m+1}}$.
∴a=|xA-xC|=|${2}^{-m}-{2}^{-\frac{8}{2m+1}}$|,b=|xB-xD|=|${2}^{m}-{2}^{\frac{8}{2m+1}}$|,
则$\frac{b}{a}$═|$\frac{{2}^{m}-{2}^{\frac{8}{2m+1}}}{{2}^{-m}-{2}^{-\frac{8}{2m+1}}}$|=2m•${2}^{\frac{8}{2m+1}}$=${2}^{m+\frac{8}{2m+1}}$,
又m>0,
∴m+$\frac{8}{2m+1}$=$\frac{1}{2}$(2m+1)+$\frac{8}{2m+1}$-$\frac{1}{2}$
≥2 $\sqrt{\frac{1}{2}(2m+1)×\frac{8}{2m+1}}$-$\frac{1}{2}$=$\frac{7}{2}$,
当且仅当 $\frac{1}{2}$(2m+1)=$\frac{8}{2m+1}$,即m=$\frac{3}{2}$时取等号,
∴$\frac{b}{a}$≥${2}^{\frac{7}{2}}$=$8\sqrt{2}$,
故选B.
点评 本题考查对数函数图象与性质,对数和指数的运算性质,平行投影的概念,以及基本不等式求最值,考查转化与数形结合的思想,化简、变形能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)<f(0)<f(4) | B. | f(-1)<f(4)<f(0) | C. | f(0)<f(-1)<f(4) | D. | f(0)<f(4)<f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知C为AB为直径的圆O上任意一点,且△SAC为等边三角形,平面SAC⊥平面ABC.
已知C为AB为直径的圆O上任意一点,且△SAC为等边三角形,平面SAC⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
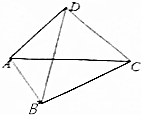 如图,在平行四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,BC=$\sqrt{3}$AB,对角线AC=2.
如图,在平行四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,BC=$\sqrt{3}$AB,对角线AC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com