
分析 (1)由题意求出直线l过定点坐标、圆心坐标,设点M(x,y),由垂径定理得MN与MC所在直线垂直,由直线斜率之积是-1列出关系式,化简后进行验证,可得弦AB的中点M的轨迹方程;
(2)设A(x1,y1),B(x2,y2),将y=kx+1代入方程(x-2)2+(y-3)2=1化简,得到一个关于x的一元二次方程,利用△>0求出k的范围,利用根与系数的关系求出4S△OAB2=|x2-x1|2=(x1+x2)2-4x1•x2,利用配方法和二次函数的性质,求出f(k)的值域.
解答 解:(1)由题意得,直线l与y轴的交点为N(0,1),圆心C(2,3),
设M(x,y),由M是弦AB的中点知:直线MN与MC所在直线垂直,
∴$\frac{y-1}{x-0}$•$\frac{y-3}{x-2}$=-1(x≠0且x≠2),化简得x2+y2-2x-4y+3=0.
当x=0时不符合题意,当x=2时y=3符合题意,
联立$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}-2x-4y+3=0}\\{(x-2)^{2}+(y-3)^{2}=1}\end{array}\right.$得,8x2-28x+21=0,
解得${x}_{1}=\frac{7-\sqrt{7}}{4}$,或${x}_{2}=\frac{7+\sqrt{7}}{4}$,
∴弦AB的中点M的轨迹方程是x2+y2-2x-4y+3=0($\frac{7-\sqrt{7}}{4}<x<\frac{7+\sqrt{7}}{4}$);
(2)设A(x1,y1),B(x2,y2),
将y=kx+1代入方程(x-2)2+(y-3)2=1得,(1+k2)x2-4(1+k)x+7=0,
∴△=16(1+k)2-28(1+k2)>0得,-3k2+8k-3>0,
解得$\frac{4-\sqrt{7}}{3}<k<\frac{4+\sqrt{7}}{3}$,
且x1+x2=$\frac{4(1+k)}{1+{k}^{2}}$,x1x2=$\frac{7}{1+{k}^{2}}$,
∵S△OAB=S△ONB-S△ONA,且|ON|=1,∴S△OAB=$\frac{1}{2}$|x2-x1|.
则4S△OAB2=|x2-x1|2=(x1+x2)2-4x1•x2
=$[\frac{4(1+k)}{1+{k}^{2}}]^{2}-4×\frac{7}{1+{k}^{2}}$=$\frac{-12{k}^{2}+32k-12}{(1+{k}^{2})^{2}}$
则S2(k)=$\frac{-12{k}^{2}+32k-12}{{4(1+{k}^{2})}^{2}}$=$\frac{-3{k}^{2}+8k-3}{{(1+{k}^{2})}^{2}}$,
∴f(k)=[S(k)•(k2+1)]2=-3k2+8k-3=$-3(k-\frac{4}{3})^{2}+\frac{7}{3}$,
∵$\frac{4-\sqrt{7}}{3}<k<\frac{4+\sqrt{7}}{3}$,
∴当k=$\frac{4}{3}$时,f(k)取到最大值为$\frac{7}{3}$,且当k=$\frac{4-\sqrt{7}}{3}或\frac{4+\sqrt{7}}{3}$时,f(k)=0,
∴f(k)的值域是(0,$\frac{7}{3}$].
点评 本题考查了直线与圆的位置关系,利用换元法求最值的基本技能,以及动点的轨迹方程,考查了设而不求思想,化简、变形能力.


科目:高中数学 来源: 题型:解答题
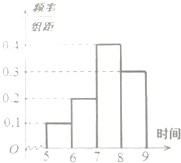 某校高三年级共有2000名学生,其中男生有1200人,女生有800人.为了了解年级学生的睡眠时间的情况,现按照分层抽样的方法从中抽取了100名学生的睡眠时间的样本数据,并绘成了如图的频率分布直方图.
某校高三年级共有2000名学生,其中男生有1200人,女生有800人.为了了解年级学生的睡眠时间的情况,现按照分层抽样的方法从中抽取了100名学生的睡眠时间的样本数据,并绘成了如图的频率分布直方图.| 性别时间 | 男生 | 女生 |
| 睡眠时间少于7小时 | ||
| 睡眠时间不少于7小时 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 9 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{3}{2}$] | B. | (0,$\frac{9}{4}$] | C. | (0,3] | D. | (0,9] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16$\sqrt{2}$ | B. | 8$\sqrt{2}$ | C. | 8$\root{3}{4}$ | D. | 4$\root{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com