
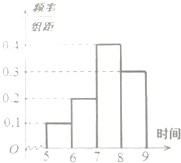
 ijУ�����꼶����2000��ѧ��������������1200�ˣ�Ů����800�ˣ�Ϊ���˽��꼶ѧ����˯��ʱ���������ְ��շֲ�����ķ������г�ȡ��100��ѧ����˯��ʱ����������ݣ����������ͼ��Ƶ�ʷֲ�ֱ��ͼ��
ijУ�����꼶����2000��ѧ��������������1200�ˣ�Ů����800�ˣ�Ϊ���˽��꼶ѧ����˯��ʱ���������ְ��շֲ�����ķ������г�ȡ��100��ѧ����˯��ʱ����������ݣ����������ͼ��Ƶ�ʷֲ�ֱ��ͼ��| �Ա�ʱ�� | ���� | Ů�� |
| ˯��ʱ������7Сʱ | ||
| ˯��ʱ�䲻����7Сʱ |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���� �ٸ��ݷֲ㶨����⼴�ɣ�
�ڸ���Ƶ��ֱ��ͼ������⣬���Ϊ1�����ÿ��ĸ��ʣ���ͼ��ɣ�
�������ʽ�е�a��b��c��d���빫ʽ��ֵ�жϼ��ɣ�
��� �⣺��100��$\frac{800}{2000}$=40�ˣ�
��P��ʱ�䲻����7Сʱ��=0.4+0.3=0.7��
������7Сʱ��Ů����5�ˣ���������25�ˣ�
a=25��b=5��c=35��d=35��
��K2=$\frac{700}{72}$��9.72��6.635��
����95%�İ�����Ϊ˯��ʱ�����Ա��йأ�
���� ���⿼���˷ֲ�����ĸ����Ƶ�ʷֲ�ֱ��ͼ�������Լ���ļ��㷽����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
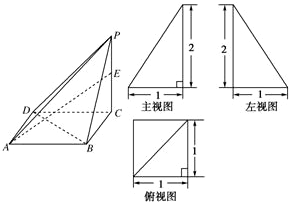 ��֪����P-ABCD������ͼ��ͼ��ʾ��E�Dz���PC�ϵĶ��㣮
��֪����P-ABCD������ͼ��ͼ��ʾ��E�Dz���PC�ϵĶ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{2}}}{2}��e-1��$ | B�� | $\sqrt{2}��e-1��$ | C�� | $\frac{{\sqrt{2}}}{2}$ | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��1�� | B�� | ��1��+�ޣ� | C�� | [2��+�ޣ� | D�� | [1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com