
分析 (Ⅰ)去绝对值,对x分类讨论,分别求解,最后求并集即可;
(Ⅱ)存在x∈R,使f(x)>|2a-4|,相当于只需f(x)的最大值大于|2a-4|,求出f(x)的最大值,解绝对值不等式即可.
解答 解:(Ⅰ)当x≤-1时,
f(x)=-4,
当-1<x<3时,
f(x)=2x-2,
当x≥3时,
f(x)=4,
∴当x≥3时f(x)≥1恒成立,
当-1<x<3时,2x-2≥1,
∴x≥$\frac{3}{2}$,
∴f(x)≥1的解集为[$\frac{3}{2}$,+∞);
(Ⅱ)由上可知f(x)的最大值为4,
∴4>|2a-4|,
∴0<a<4,
故a的范围为(0,4).
点评 考查了绝对值函数的求解和恒成立问题的转化,属于基础题型,应熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
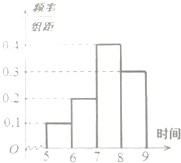 某校高三年级共有2000名学生,其中男生有1200人,女生有800人.为了了解年级学生的睡眠时间的情况,现按照分层抽样的方法从中抽取了100名学生的睡眠时间的样本数据,并绘成了如图的频率分布直方图.
某校高三年级共有2000名学生,其中男生有1200人,女生有800人.为了了解年级学生的睡眠时间的情况,现按照分层抽样的方法从中抽取了100名学生的睡眠时间的样本数据,并绘成了如图的频率分布直方图.| 性别时间 | 男生 | 女生 |
| 睡眠时间少于7小时 | ||
| 睡眠时间不少于7小时 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在四棱锥P-ABCD中,PA⊥平面ABCD,PA=2AB=2,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点,在平面PCD内作EF⊥PC于点F.
在四棱锥P-ABCD中,PA⊥平面ABCD,PA=2AB=2,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,E为PD的中点,在平面PCD内作EF⊥PC于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com